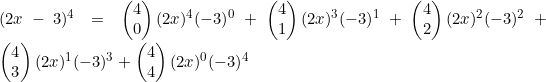A brumby is a free-roaming wild horse found in large number in parts of Australia. The culling of brumbies was banned in the year 2000. At this time the estimated population of brumbies in
Kosciuszko National Park was 1600. Scientists have modelled the population, P(t), of brumbies in
Kosciuszko National Park t years since the ban, by
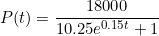
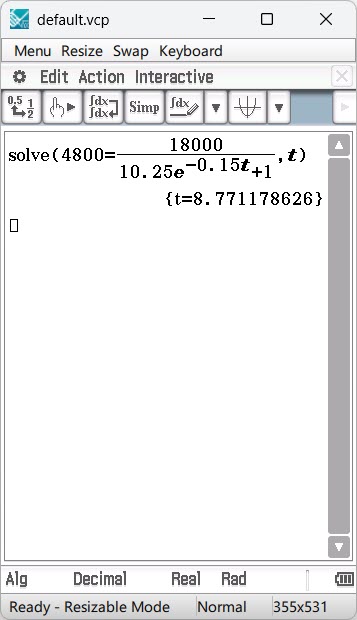
(a) Use the model to determine how long it will take the brumbies to increase to a number that is triple the number when the ban came into effect.
(b) From this model, determine the estimated long run number of brumbies in Kosciuszko National Park.
It can be shown that the growth rate of the population of brumbies can be expressed as
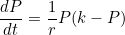
(c) Determine the values of the constants  and
and 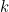 .
.
(d) Determine the greatest growth rate for the population of brumbies.
ATAR 2024 Specialist Mathematics Question 13
(a) 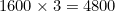
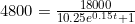
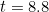 years.
years.
(b) 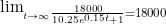
(c)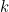 is the carrying capacity (long run number of Brumbies), therefore
is the carrying capacity (long run number of Brumbies), therefore 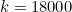 .
.
Remember,
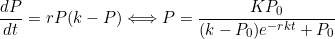
We have 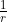 instead of
instead of  .
.
Therefore,
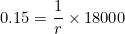
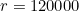
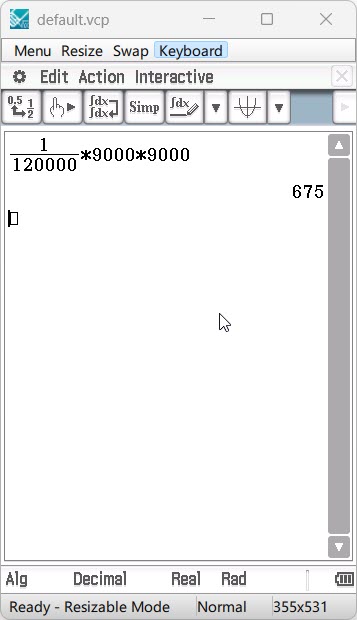
(d) The greatest growth rate occurs when 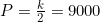
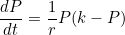
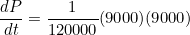
The greatest growth rate is 675 Brumbies per year.
![]()
![]()
![]() )
)![]()
![]() ) and subtract the square of the second term.
) and subtract the square of the second term.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


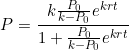
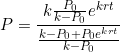
 and
and 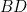 are added
are added