May 12, 2024 · 11:50 am

Fractions to decimals

People usually know some fractions as decimals, for example

    \[\frac{1}{4}=0.25\ \textnormal{or }\frac{4}{5}=0.8\]

And denominators that are powers of ten are also easy,

    \[\frac{47}{100}=0.47\ \textnormal{or }\frac{256}{1000}=0.256\]

But what if it is something else? One that you don’t know. For example,

    \[\frac{5}{12}\ \textnormal{or }\frac{15}{37}\]

I like to do these as a long division

Leave a Comment

Filed under Arithmetic, Decimals, Fractions

Tagged as , ,

May 9, 2024 · 6:08 am

Intersections of Lines and Circles

The three possibilities: no intersection, one point of intersection, or two points of intersection

Once my students have studied circle and quadratic equations, I like to introduce lines intersecting with circles. It tests their quadratic equation solving skills, and if they can use the discriminant.

Example 1

Calculate the point(s) of intersection of

    \[3x+2y-6=0\ \textnormal{and}\ (x+4)^2+(y+2)^2=9\]

Rearrange the line equation

    \[y=\frac{6-3x}{2}\]

    \[y=3-\frac{3x}{2}\]

Substitute for y into the circle equation

    \[(x+4)^2+(3-\frac{3x}{2}+2)^2=9\]

    \[(x+4)^2+(5-\frac{3x}{2})^2=9\]

    \[x^2+8x+16+25-15x+\frac{9x^2}{4}-9=0\]

    \[\frac{13x^2}{4}-7x+32=0\]

    \[13x^2-28x+128=0\]

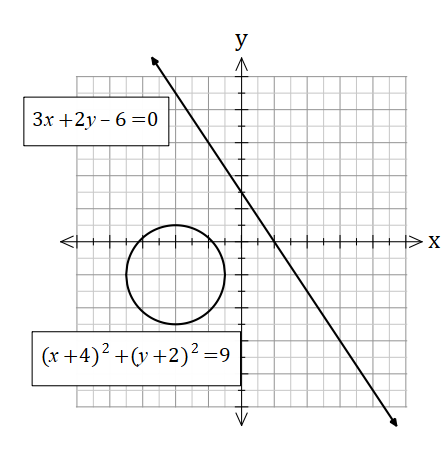
At this point I like to check the discrimnant

    \[\Delta=b^2-4ac\]

    \[\Delta=(-28)^2-4\times13\times128\]

    \[\Delta=-5872\]

As the discriminate is less than zero, there are no points of intersection.

Example 2

Calculate the point(s) of intersection of

    \[y=2x+1\ \textnormal{and}\ (x+5)^2+(y+3)^2=16\]

    \[(x+5)^2+(2x+1+3)^2=16\]

    \[(x+5)^2+(2x+4)^2=16\]

    \[x^2+10x+25+4x^2+16x+16-16=0\]

    \[5x^2+26x+25=0\]

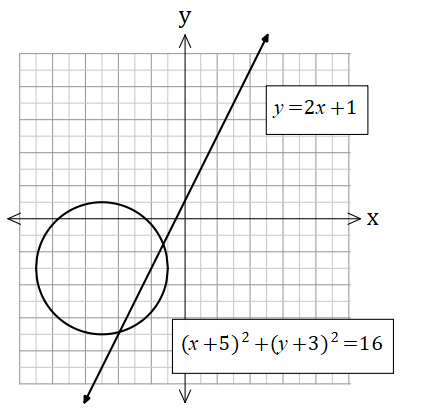
Check the discriminant

    \[\Delta=26^2-4\times5\times25\]

    \[\Delta=176\]

Therefore there are two points of intersection

    \[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]

    \[x=\frac{-26\pm\sqrt{176}}{10}\]

    \[x=\frac{-26\pm4\sqrt{11}}{10}\]

    \[x=\frac{-13\pm2\sqrt{11}}{5}\]

Substitute x into y

    \[y=2(\frac{-13\pm2\sqrt{11}}{5})+1\]

    \[\textnormal{The two points are}\ (\frac{-13+2\sqrt{11}}{5},\frac{-21+4\sqrt{11}}{5})\]

    \[\textnormal{and}\ (\frac{-13-2\sqrt{11}}{5},\frac{-21-4\sqrt{11}}{5})\]

Example 3

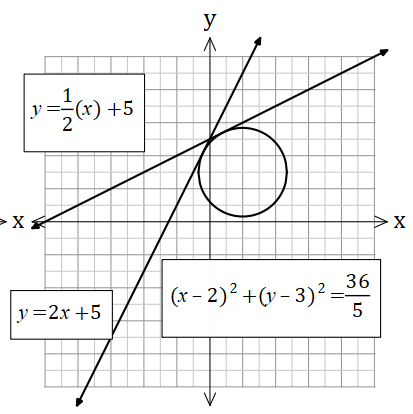
Find the value of k so that the line and the circle intersect at one point (i.e. the line is a tangent to the circle)

    \[-kx+y-5=0\ \textnormal{and}\ (x-2)^2+(y-3)^2=\frac{36}{5}\]

    \[y=kx+5\]

    \[(x-2)^2+(kx+5-3)^2=\frac{36}{5}\]

    \[(x-2)^2+(kx+2)^2=\frac{36}{5}\]

    \[x^2-4x+4+k^2x^2+4kx+4-\frac{36}{5}=0\]

    \[(1+k^2)x^2+(4k-4)x+\frac{4}{5}=0\]

Find the discriminant (remember for one solution we want the discriminant to be zero)

    \[\Delta=b^2-4ac\]

    \[\Delta=(4k-4)^2-4\times(1+k^2)\times\frac{4}{5}\]

    \[\Delta=16k^2-32k+16-\frac{16}{5}-\frac{16k^2}{5}\]

    \[0=16k^2-32k+16-\frac{16}{5}-\frac{16k^2}{5} \[0=80k^2-160k+80-16-16k^2\]

    \[0=64k^2-160k+64\]

    \[0=32(2k^2-5k+2)\]

    \[0=2k^2-5k+2\]

    \[0=2k^2-4k-k+2\]

    \[0=2k(k-2)-1(k-2)\]

    \[0=(2k-1)(k-2)\]

    \[k=\frac{1}{2}\ \textnormal{and}\ k=2\]

Leave a Comment

Filed under Circles and Quadratics, Quadratics

Tagged as , ,

May 2, 2024 · 9:54 am

Napoleon’s Theorem

This is one of those theorems, where the name is probably not the person who discovered it. Check out the Wikipedia entry for more information on the history.

Napoleon’s theorem states that if equilateral triangles are constructed on the sides of any triangle, either all outward or all inward, the lines connecting the centres of those equilateral triangles themselves form an equilateral triangle.

I am just going to look at the outward triangles.

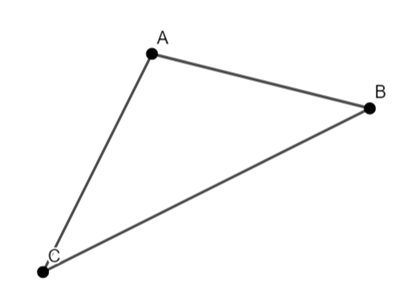
Construct equilateral triangles on the edges AB, BC and AC.

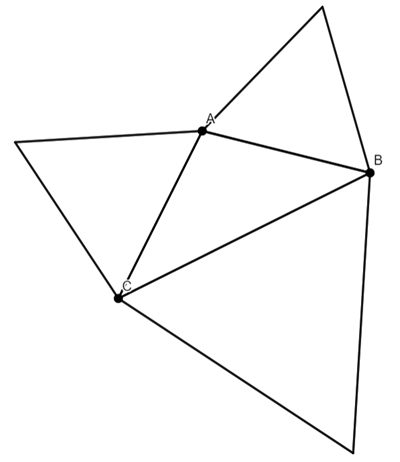
Find the centre (Centroid) of these triangles.

Note: The centroid is the point of intersections of the medians.

A median is the line from a vertex to the midpoint of the opposite side.

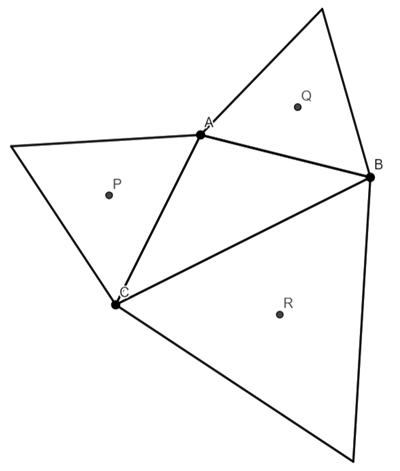
We are going to prove that triangle PQR is equilateral

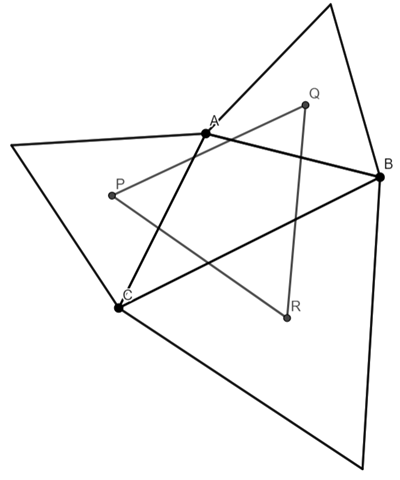
I am going to add AP, AQ, QB, BR, RC and CP

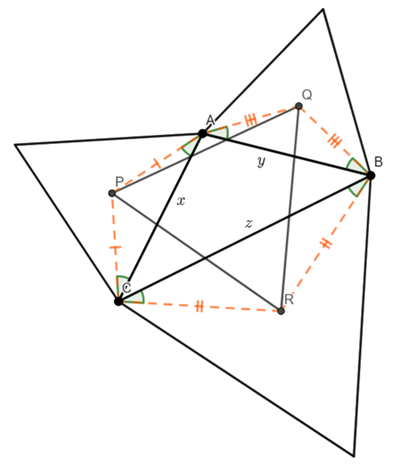
As P, Q and R are the centroids, PA=PC, QA=QB, and RB=RC.

Therefore triangles AQB, BRC, and CPA are isosceles.

The angles QAB, QBA, RBC, RCB, PCA, PAC (the shaded angles in the above diagram) are 30 degrees, because the line bisects the angle (and the angle is 60 degrees because the triangles are equilateral).

Now for the maths.

    \[\textnormal {Let}\ AB=y,\ AC=x,\ BC=z\]

    \[\textnormal {Let}\ \angle{CAB}=\theta,\ \angle{ABC}=\alpha,\ \angle{BCA}=\gamma\]

    \[\therefore\angle{PAQ}=(60+\theta),\ \angle{QBR}=(60+\alpha),\]

    \[ \angle{RCP}=(60+\gamma)\]

PA is 2/3 the length of the median.

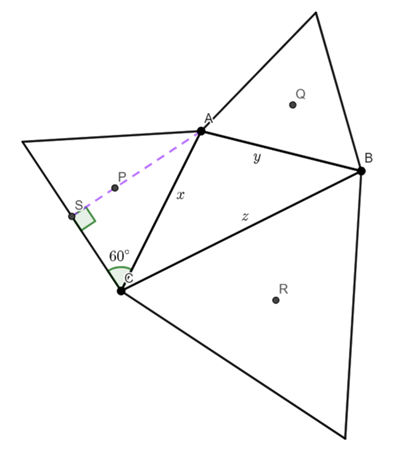
AS is the median

    \[sin(60)=\frac{AS}{x}\]

    \[AS=xsin(60)\]

    \[AS=\frac{\sqrt{3}}{2}x\]

Hence,

    \[PA=\frac{2}{3}\frac{\sqrt3}{2}x\]

    \[PA=\frac{\sqrt{3}}{3}x\]

    \[PA=\frac{x}{\sqrt{3}}\]

In the same manner,

    \[QA=\frac{y}{\sqrt{3}}\ \textnormal {and} \ BR=\frac{z}{\sqrt{3}}\]

Using the cosine rule

    \[(PQ)^2=(\frac{x}{\sqrt{3}})^2+(\frac{y}{\sqrt{3}})^2-2\frac{x}{\sqrt{3}}\frac{y}{\sqrt{3}}cos(60+\theta)\]

    \[(PQ)^2=\frac{x^2}{3}+\frac{y^2}{3}-\frac{2xy}{3}cos(60+\theta)\]

    \[\textnormal{Use a trigonometric identity to expand}\ cos(60+\theta)\]

    \[(PQ)^2=\frac{x^2}{3}+\frac{y^2}{3}-\frac{2xy}{3}(cos60cos\theta-sin60sin\theta)\]

    \[(PQ)^2=\frac{x^2}{3}+\frac{y^2}{3}-\frac{2xy}{3}(\frac{1}{2}cos\theta-\frac{\sqrt{3}}{2}sin\theta)\]

Now from the original triangle ABC

    \[cos\theta=\frac{x^2+y^2-z^2}{2xy}\ \textnormal {and}\ A=\frac{1}{2}xysin\theta\ \textnormal {where} A\ \textnormal {is the area.}\]

    \[\textnormal{Substitute into}\ (PQ)^2 \]

    \[(PQ)^2=\frac{x^2}{3}+\frac{y^2}{3}-\frac{2xy}{3}(\frac{x^2+y^2-z^2}{4xy}-\frac{\sqrt{3}A}{xy})\]

Multiply both sides by 3 and expand and simplify

    \[3(PQ)^2=x^2+y^2-2xy(\frac{x^2+y^2-z^2}{4xy}-\frac{\sqrt{3}A}{xy})\]

    \[3(PQ)^2=x^2+y^2-(\frac{x^2}{2}+\frac{y^2}{2}-\frac{z^2}{2}-2\sqrt{3}A)\]

    \[3(PQ)^2=\frac{x^2}{2}+\frac{y^2}{2}+\frac{z^2}{2}+2\sqrt{3}A\]

We are going to do the same for QR

    \[(QR)^2=\frac{y^2}{3}+\frac{z^2}{3}-\frac{2yz}{3}(cos(60+\alpha)\]

    \[(QR)^2=\frac{y^2}{3}+\frac{z^2}{3}-\frac{2xy}{3}(cos60cos\alpha-sin60sin\alpha)\]

    \[(QR)^2=\frac{y^2}{3}+\frac{z^2}{3}-\frac{2xy}{3}(\frac{1}{2}cos\alpha-\frac{\sqrt{3}}{2}sin\alpha)\]

Once again, from triangle ABC

    \[cos\alpha=\frac{y^2+z^2-x^2}{2yz}\ \textnormal {and}\ A=\frac{1}{2}zysin\alpha\ \textnormal {where} A\ \textnormal {is the area.}\]

    \[\textnormal{Substitute into}\ (QR)^2 \]

    \[(QR)^2=\frac{y^2}{3}+\frac{z^2}{3}-\frac{2yz}{3}(\frac{y^2+z^2-x^2}{4yz}-\frac{\sqrt{3}A}{yz})\]

Multiply both sides by three and expand and simplify

    \[3(QR)^2=y^2+z^2-2yz(\frac{y^2+z^2-x^2}{4yz}-\frac{\sqrt{3}A}{yz})\]

    \[3(QR)^2=y^2+z^2-(\frac{y^2}{2}+\frac{z^2}{2}-\frac{x^2}{2}-2\sqrt{3}A)\]

    \[3(QR)^2=\frac{x^2}{2}+\frac{y^2}{2}+\frac{z^2}{2}+2\sqrt{3}A\]

We can do the same for PR

    \[(PR)^2=\frac{x^2}{3}+\frac{z^2}{3}-\frac{2xz}{3}cos(60+\gamma)\]

    \[(PR)^2=\frac{x^2}{3}+\frac{z^2}{3}-\frac{2xz}{3}(cos60cos\gamma-sin60sin\gamma)\]

    \[(PR)^2=\frac{x^2}{3}+\frac{z^2}{3}-\frac{2xz}{3}(\frac{1}{2}cos\gamma-\frac{\sqrt{3}}{2}sin\gamma)\]

And from triangle ABC

    \[cos\gamma=\frac{x^2+z^2-y^2}{2xz}\ \textnormal{and}\ A=\frac{1}{2}sin\gamma\ \textnormal{where A is the area.}\]

    \[\textnormal{substitute into}\ (PR)^2\]

    \[(PR)^2=\frac{x^2}{3}+\frac{y^2}{3}-\frac{2xz}{3}(\frac{x^2+z^2-y^2}{4xz}-\frac{\sqrt{3}A}{xz})\]

Multiply both sides by three and expand and simplify

    \[3(PR)^2=\frac{x^2}{2}+\frac{y^2}{2}+\frac{z^2}{2}+2\sqrt{3}A\]

Hence, PQ=PR=RQ and triangle PQR is equilateral.

Leave a Comment

Filed under Interesting Mathematics, Napoleon's Triangle

April 17, 2024 · 9:32 am

Sketching Subsets of the Complex Plane – Problem 2

I found this question on the madasmaths site – his resources are fabulous.

I am not sure I would have been able to do this in an exam.

I have split my solution into 6 images and there is a pdf version at the bottom

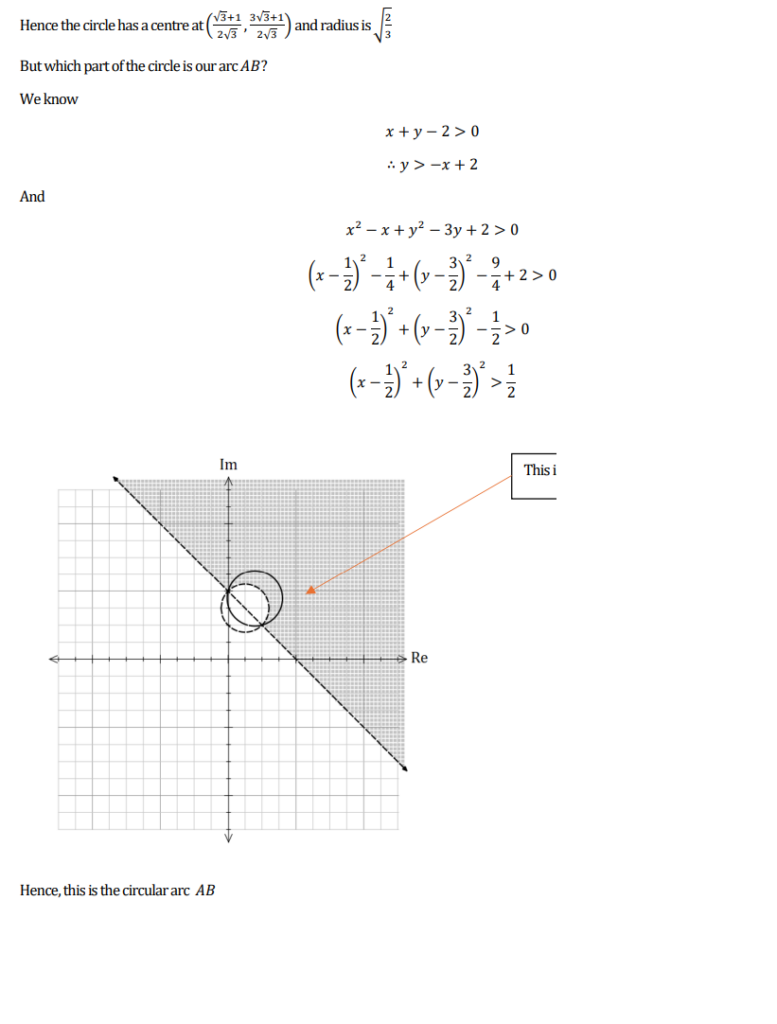
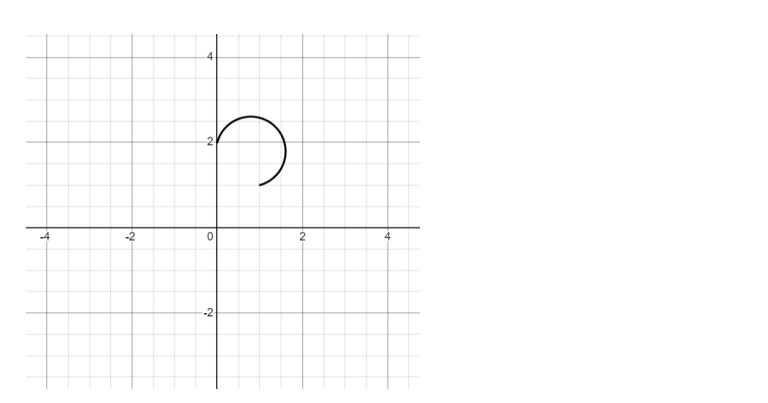
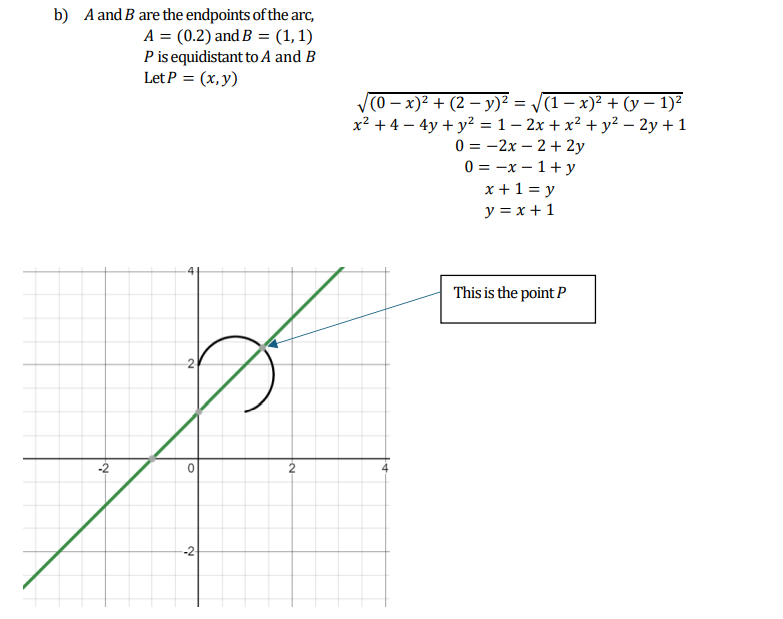
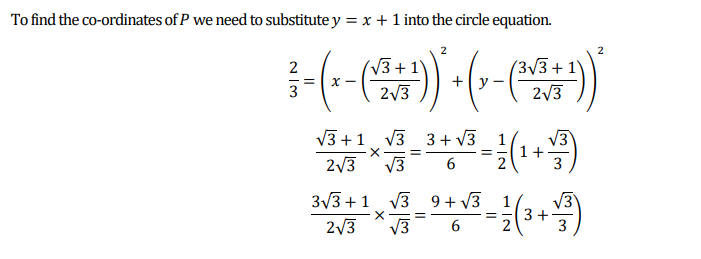
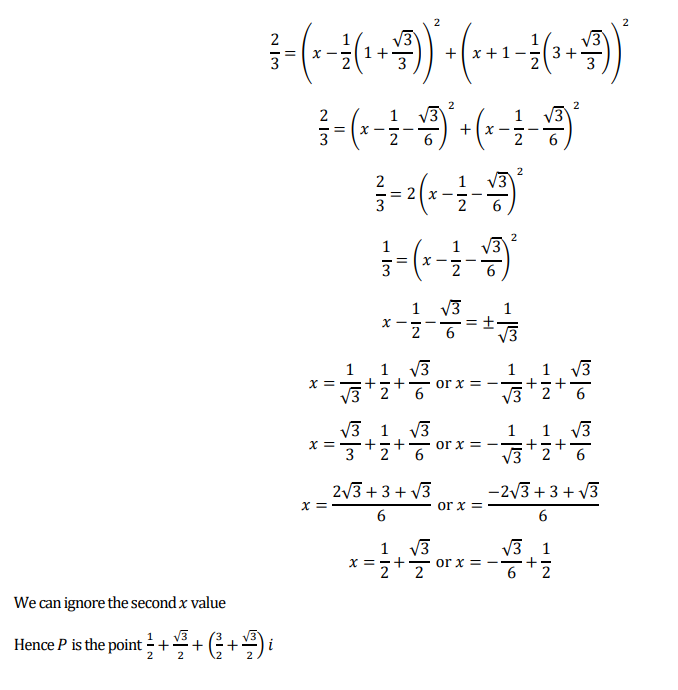
PDF version of my solution

Leave a Comment

Filed under Complex Numbers, Sketching Complex Regions

Tagged as , ,

April 14, 2024 · 6:35 am

Divisibility Rules – Integers 1 to 10

I think it’s useful to knot the divisibility rules, at least up to ten. Although, let’s face it, 7 is a bit tricky.

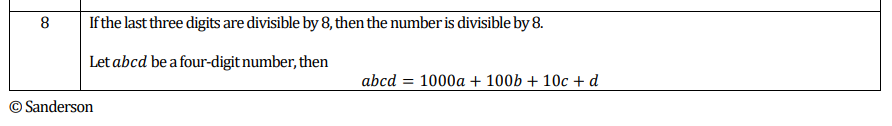
Divisibility Rules pdf

1 Comment

Filed under Arithmetic, Divisibility

Tagged as ,

April 10, 2024 · 7:45 am

Integrating by Trigonometric Substitution

Integrating by using a trigonometric substitution can be quite trick for some students.

For example, this question from OCR 4726 June 2009 Question 6

Trig Substitution Notes

PDF version of the above solution

Leave a Comment

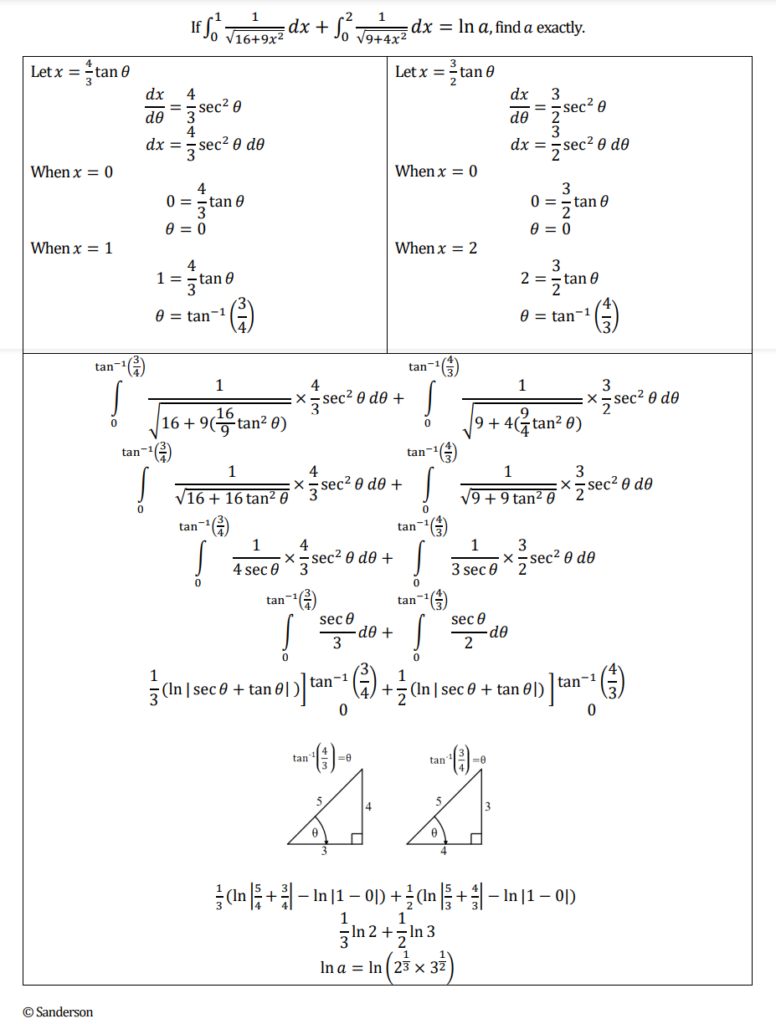
Filed under Integration, Trigonometric Substitution

Tagged as , ,

April 2, 2024 · 7:10 am

Factorising Non-Monic Trinomials

I factorise trinomials by using the grouping method, I will show you what I mean

But one of my students showed me a different way

I have put in more steps than is necessary. I think this might be a quicker method.

Leave a Comment

Filed under Factorising, Quadratics

Tagged as ,

March 31, 2024 · 8:27 am

Sketching Subsets of the Complex Plane – Problem 1

Describe the locus defined by

A pdf version.

Leave a Comment

Filed under Uncategorized

March 29, 2024 · 6:20 am

Three Circles – Area Problem

This is question 5 from the UK Maths Trust Senior Challenge October 2023.

I have tackled this in three ways; using non-right trig to find the area, Heron’s Law, and the Shoelace Formula.

Method 1

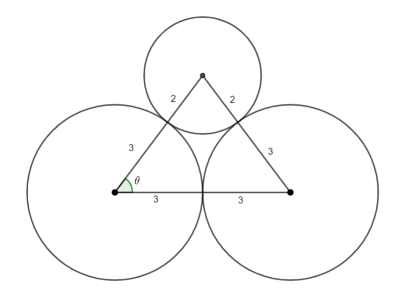
Use the area of a triangle formula

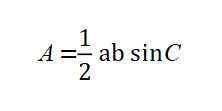
Use the cosine rule to find cosθ.

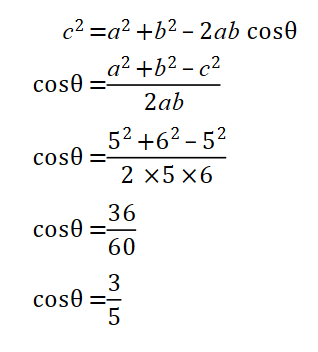
Once we have cosθ, we can find sinθ.

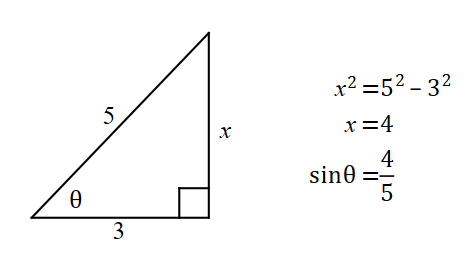
Hence the area is,

Method 2

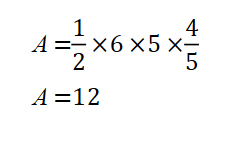
Use Heron’s law.

Heron’s law is a way of calculating area of a triangle from the lengths of the three sides of the triangle.

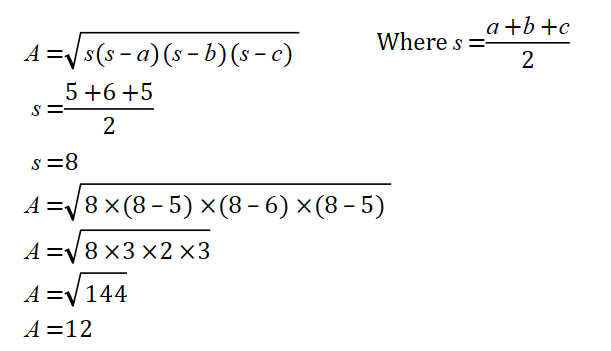
This is my preferred method – simple and direct.

Method 3

Shoelace formula (Gauss’s Area formula)

We need to allocate each of the vertices a co-ordinate.

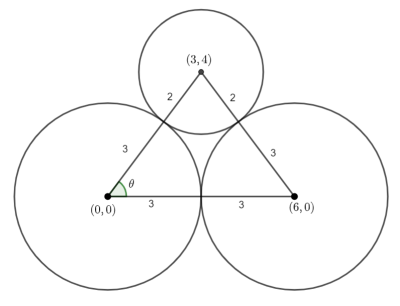
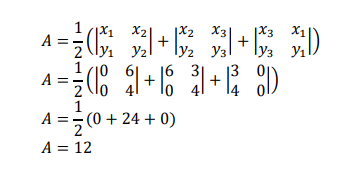
The co-ordinates are listed in an anti-clockwise direction.

This is probably a bit over the top, but once you get the hang of it, it’s very easy.

Leave a Comment

Filed under Area, Area of Triangles (Sine), Heron's Law, Non-Right Trigonometry, Shoelace Forumla, Trigonometry

Tagged as , ,

March 28, 2024 · 8:54 am

Midpoint

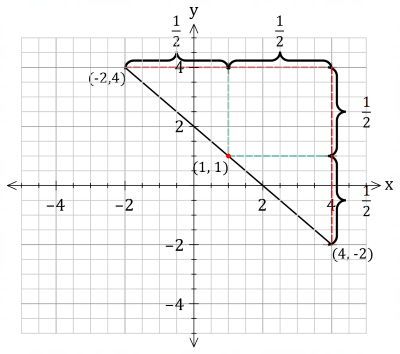
I find many students struggle with the formal notation for calculating midpoint.

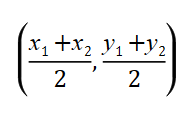
The idea of finding halfway between the x and y co-ordinates seems to resonate.

You can then introduce the formula and use that as a way of getting to grips with the distance formula and the gradient formula.

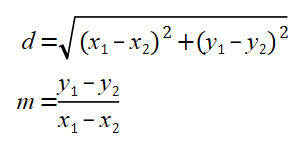
My notes on midpoint.

My notes on gradient.

More on gradient distance between points later.

Leave a Comment

Filed under Co-ordinate Geometry

Tagged as