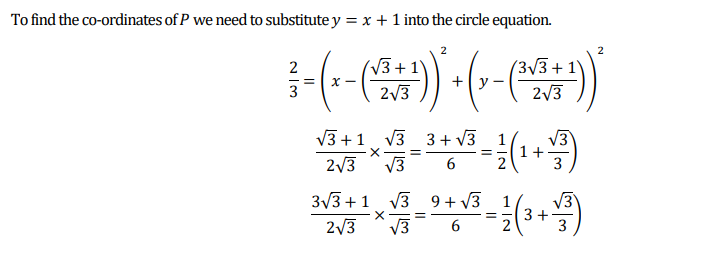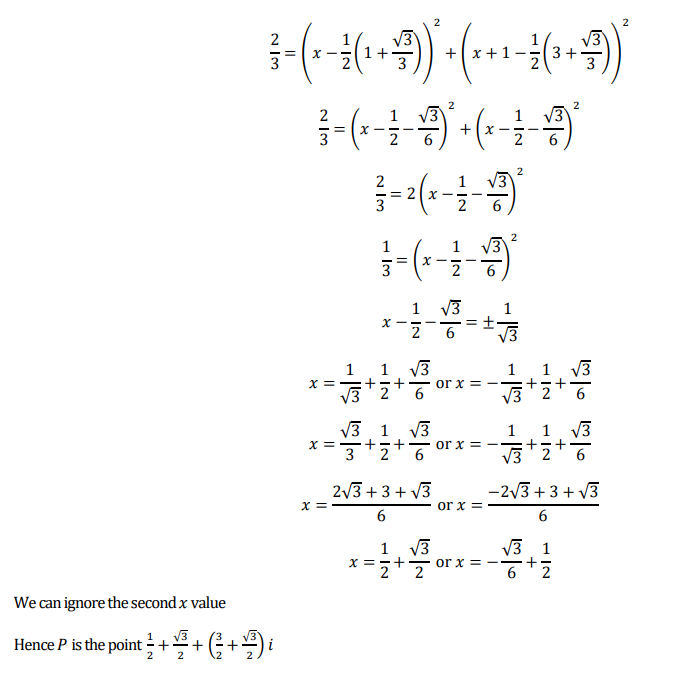I have been reading An Imaginary Tale – The Story of  by Paul J Nahin, which is fabulous. There was a bit in chapter 4 where he found the closed form of the generalised Fibonacci sequence. I thought it would be a good exercise to find the closed from of the Fibonacci sequence.
by Paul J Nahin, which is fabulous. There was a bit in chapter 4 where he found the closed form of the generalised Fibonacci sequence. I thought it would be a good exercise to find the closed from of the Fibonacci sequence.
Just to remind you, the Fibonacci sequence is
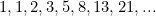
and it is defined recursively
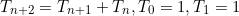
That is, the next term is the sum of the two previous terms, i.e.
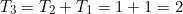
Now the starting off point is slightly dodgy as it involves and educated guess as Paul Nahin writes,
How do I know that works? Because I have seen it before, that’s how! […] There is nothing dishonourable about guessing correct solutions – indeed, great mathematicians and scientists, are invariable great guessers – just as long as eventually the guess is verified to work. The next time you encounter a recurrence formula, you can guess the answer too because then you will have already seen how it works.
We start with 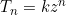
This means 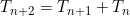 is
is 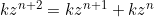
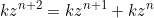
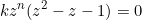
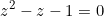
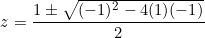
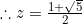 or
or 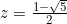
Hence 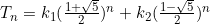 and we can use the initial conditions
and we can use the initial conditions 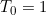 and
and 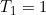 to find
to find 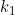 and
and 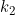
When 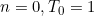
(1) 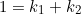
When 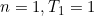
(2) 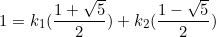
From equation  ,
, 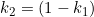 , substitute into equation
, substitute into equation 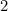
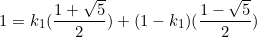
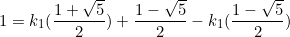

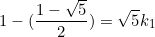
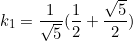
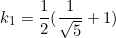
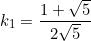
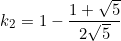
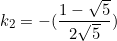
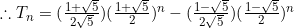
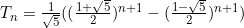
Does it work?
Remember the sequence is 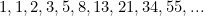
If 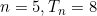
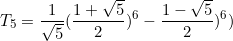
As you can see it works!
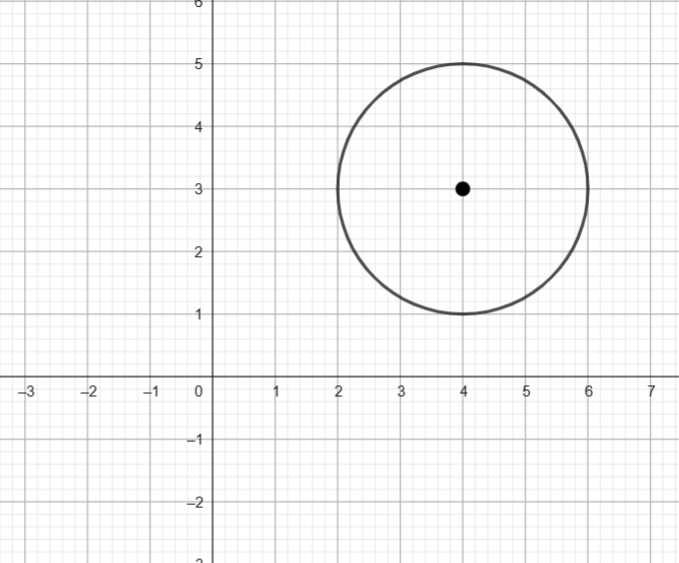
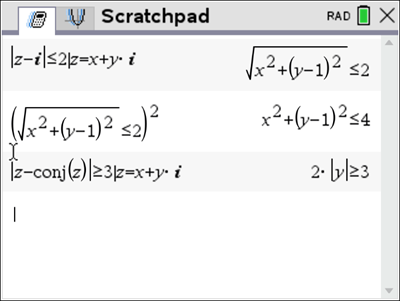
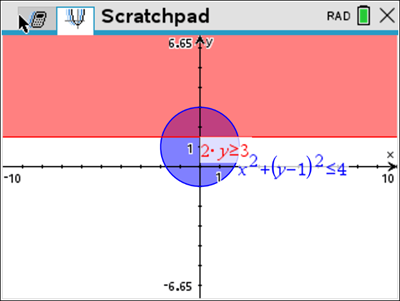
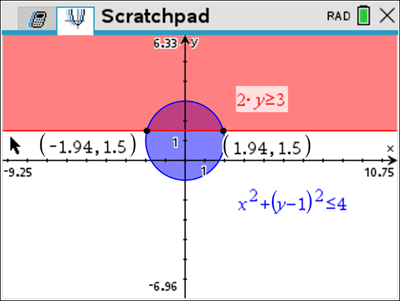
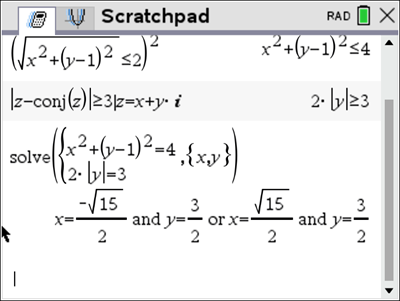
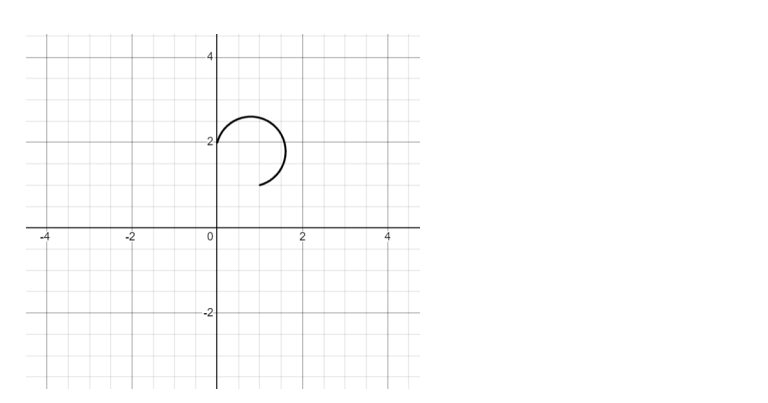
![]() is shown above, determine the maximum value of
is shown above, determine the maximum value of ![]() correct to two decimal places where
correct to two decimal places where ![]()
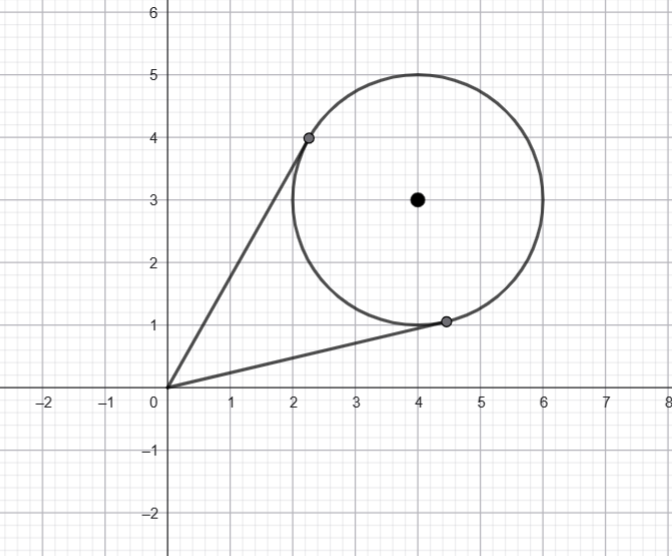
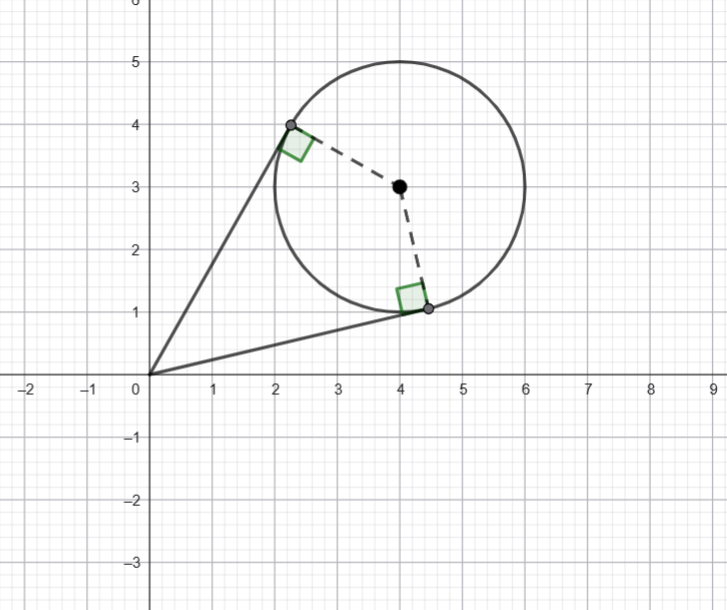
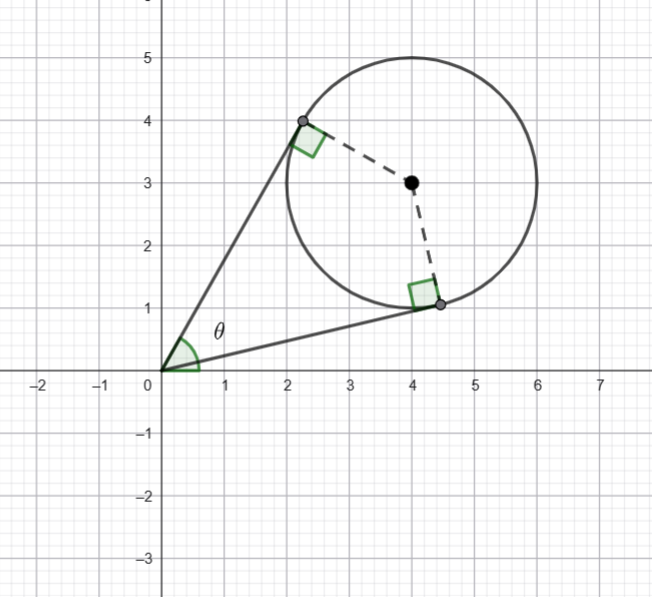
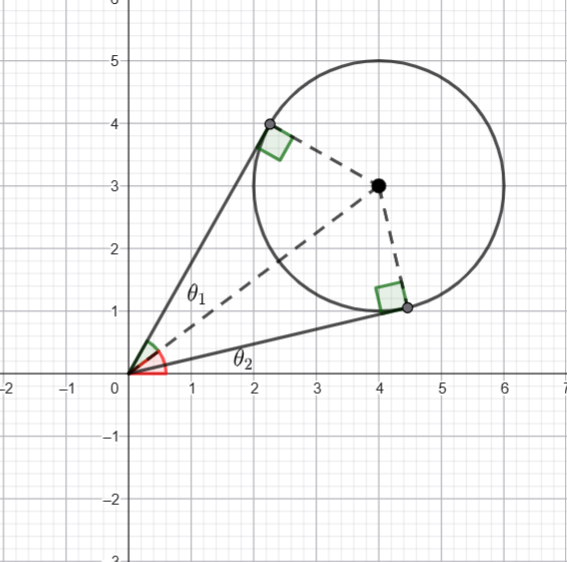
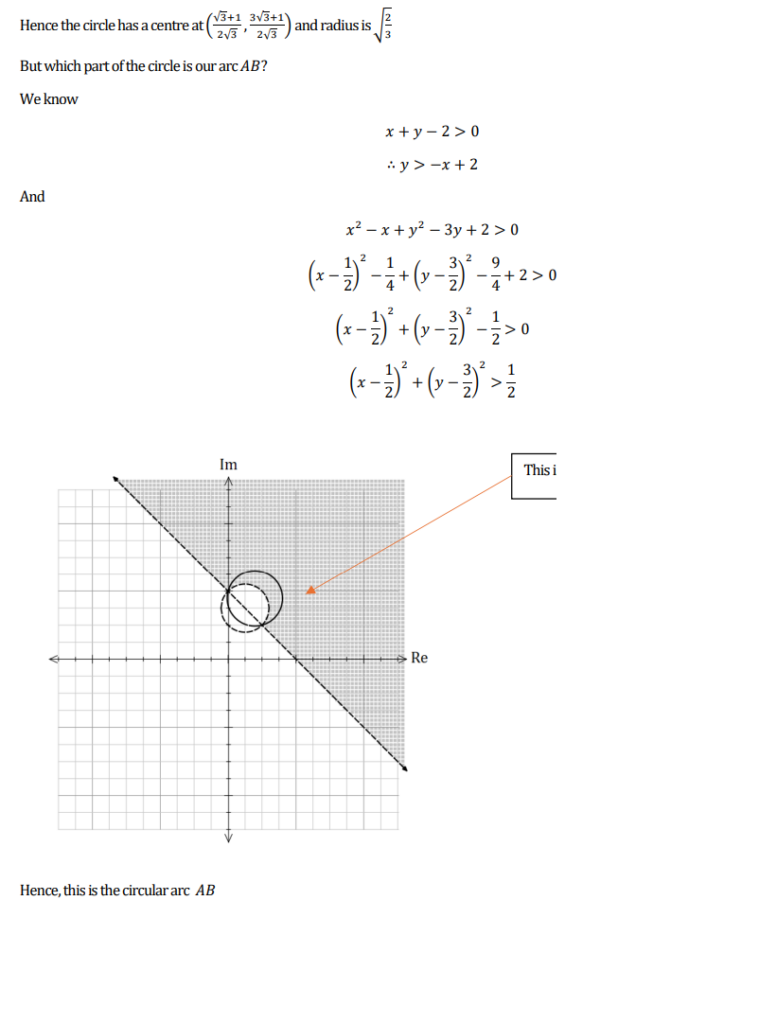
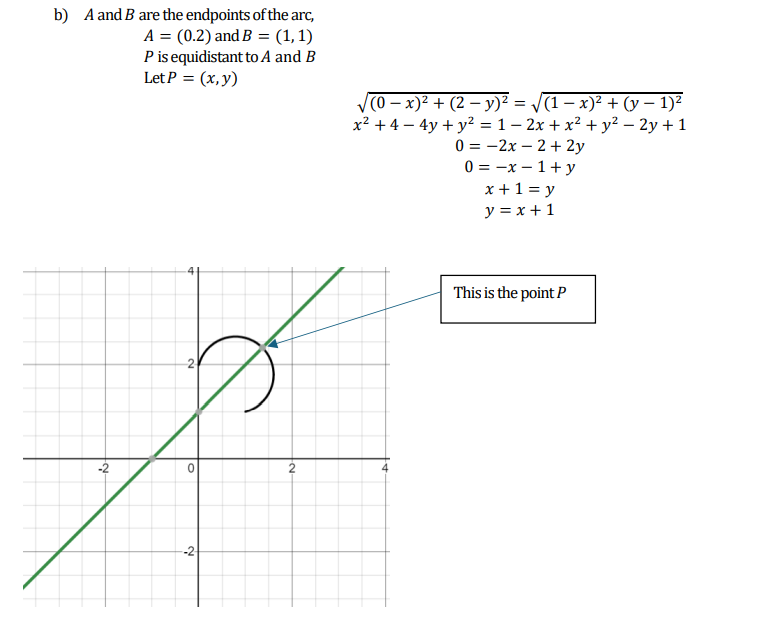
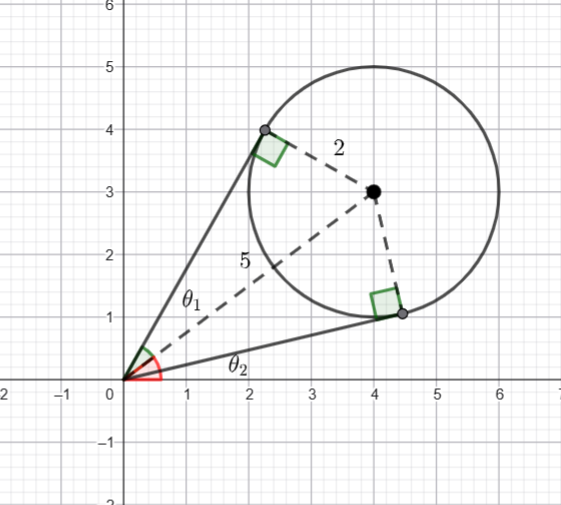
![]() and the centre is
and the centre is ![]() . Hence the distance from the origin to the centre is
. Hence the distance from the origin to the centre is ![]() .
.
![]()
![]()
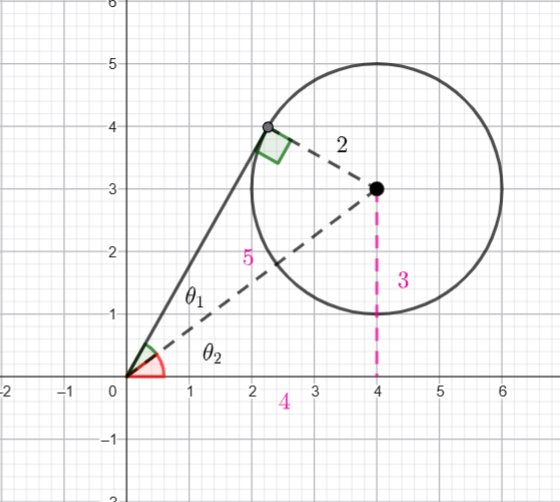
![]()
![]()
![]()