Category Archives: Solving

November 22, 2025 · 6:10 am

Polynomial Long Division

I usually choose to use synthetic division when factorising polynomials, but I know some teachers are unhappy when their students do this. So for completeness, here is my PDF for Polynomial Long Division.

Polynomial Long Division Download

Hard Equation Solving Question

Find the value(s) of $k$ such that the equation below has two numerically equal but opposite sign solutions (e.g. $5$ and $-5$ ).

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{k-1}{k+1}\end{equation}$

$\begin{equation*}(x^2-2x)(k+1)=(k-1)(4x-1)\end{equation}$

$\begin{equation*}(k+1)x^2-2kx-2x=4kx-k-4x+1\end{equation}$

$\begin{equation*}(k+1)x^2-2kx-4kx-2x+4x-1=0\end{equation}$

$\begin{equation*}(k+1)^2x^2-(6k-2)x-1=0\end{equation}$

For there to be two numerically equal but opposite sign solutions, the $b$ term of the quadratic equation must be $0$ .

$\begin{equation*}6k-2=0\end{equation}$

Hence $k=\frac{1}{3}$ .

When $k=\frac{1}{3}$ the equation becomes

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{\frac{-2}{3}}{\frac{4}{3}}\end{equation}$

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{-1}{2}\end{equation}$

$\begin{equation*}2x^2-4x=-4x+1\end{equation}$

$\begin{equation*}2x^2-1=0\end{equation}$

$\begin{equation*}x^2=\frac{1}{2}\end{equation}$

$\begin{equation*}x=\pm \frac{1}{\sqrt{2}}\end{equation}$

Simultaneous Equation (or is it?)

Solve simultaneously

$X+Y+Z=10$
$XYZ=30$
$XY+YZ+XZ=31$

We could attempt to solve this simultaneously, but I think the algebra would be tricky.

The three equations are related to the roots of a cubic polynomial.

If the general equation of the polynomial is $ax^3+bx^2+cx+d$ , then we know

The sum of the roots

The product of the roots

and

\alpha\beta+\alpha\gamma+\beta\gamma=\frac{c}{a}

So from our three equations we have

(1) $\begin{equation*}X+Y+Z=10=\frac{-b}{a}\end{equation*}$

(2) $\begin{equation*}XYZ=30=\frac{-d}{a}\end{equation*}$

(3) $\begin{equation*}XY+YZ+XZ=31=\frac{c}{a}\end{equation*}$

Let $a=1$ , then $b=-10, c=31$ , and $d=-30$

Our cubic is $t^3-10t^2+31t-30$ and we can try to solve it.

The roots will be factors of $-30$ , so $\pm 1, \pm 2, \pm 3, \pm 5, \pm 6, \pm 10, \pm 15, \pm 30$

Try $t=2$

$\begin{equation*}(2)^3-10(2)^2+31(2)-30=0\end{equation}$

Hence $t=2$ is a root.

Use synthetic division to find the quadratic factor

$2$	$1$	$-10$	$31$	$-30$
		$2$	$-16$	$30$
	$1$	$-8$	$15$	$0$

The quadratic factor is $x^2-8x+15$ , which factorises to $(x-3)(x-5)$

Hence the solutions are $X=2, Y=3$ , and $Z=5$

We could assume the solutions are natural numbers, then we can look at factors of 30.

Hence the solutions are $X=2, Y=3,$ and $Z=5$

But with this approach we might not be able to find the solutions.

Deriving the Quadratic Equation formula

My year 10 students have been learning how to complete the square with the idea of then deriving the quadratic equation formula.

The general equation for a quadratic is $y=ax^2+bx+c$

Completing the square,

$\begin{equation*}ax^2+bx+c\end{equation}$

Factorise out the leading coefficient (i.e. $a$ )

$\begin{equation*}a(x^2+\frac{bx}{a}+\frac{c}{a})\end{equation}$

Half the second term (i.e $\frac{b}{a}$ ) and subtract the square of the second term.

$\begin{equation*}a((x+\frac{b}{2a})^2-(\frac{b}{2a})^2+\frac{c}{a})\end{equation}$

$\begin{equation*}a((x+\frac{b}{2a})^2-\frac{b^2}{4a^2}+\frac{c}{a})\end{equation}$

Simplify

$\begin{equation*}a((x+\frac{b}{2a})^2-\frac{b^2}{4a^2}+\frac{4ac}{4a^2})\end{equation}$

$\begin{equation*}a((x+\frac{b}{2a})^2+\frac{-b^2+4ac}{4a^2})\end{equation}$

$\begin{equation*}a(x+\frac{b}{2a})^2+\frac{-b^2+4ac}{4a}\end{equation}$

Now let’s solve

$\begin{equation*}a(x+\frac{b}{2a})^2+\frac{-b^2+4ac}{4a}=0\end{equation}$

$\begin{equation*}a(x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a}\end{equation}$

$\begin{equation*}(x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a^2}\end{equation}$

$\begin{equation*}(x+\frac{b}{2a})=\pm \sqrt{\frac{b^2-4ac}{4a^2}}\end{equation}$

$\begin{equation*}(x+\frac{b}{2a})=\frac{\pm \sqrt{b^2-4ac}}{2a}\end{equation}$

$\begin{equation*}x=-\frac{b}{2a}\frac{\pm \sqrt{b^2-4ac}}{2a}\end{equation}$

Which is the quadratic equation formula.

1 Comment

Filed under Algebra, Quadratic, Quadratics, Solving, Solving, Solving Equations

Tagged as completing the square, quadratic equation formula

September 19, 2024 · 9:43 am

Solving Cubic Functions

I have been thinking about cubics a bit lately because some of my students are solving and then sketching cubics. Plus I am reading An Imaginary Tale by Paul Nahin, which talks about solving cubics and complex numbers.

Cubics must have at least one real root. If one of the roots is a rational number, then we can use the Factor and Remainder Theorem.

For example,

Solve $2x^3-3x^2-3x+2=0$

But what if it is not factorisable?

For example,

Solve $2x^3+5x^2-2x+4=0$

How many roots does this equation have?

We could find the derivative and find out how many stationary points the function has.

$f'(x)=6x^2+10x-2$

This is a quadratic function. Find the discriminant to determine the number of roots.

$\Delta=b^2-4ac=100-4(6)(-2)=148$

As $\Delta>0$ , there are two stationary points, which means we could have 1, 2 (one root is repeated) or three roots, depending on if the function crosses the $x-$ axis between stationary points. So not much use.

We could try the discriminant of a cubic.

$\Delta=18abcd-4b^3d+b^2c^2-4ac^2-27a^2d^2$

$\Delta=18(2)(5)(-2)(4)-4(5^3)(4)+(5^2)(-2)^2-4(2)(-2)^2-27(2)^2(4)^2=-5100$

The discriminant is negative so there is one real root.

From my reading, we need to turn the cubic into a depressed cubic (cubics of the form $x^3+px+q=0$ ).

We can do this by using a change of variable.

We can then use Cardano’s formula

$x=\sqrt[3]{-\frac{q}{2}+\sqrt{(-\frac{q}{2})^2+(\frac{p}{3})^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{(-\frac{q}{2})^2+(\frac{p}{3})^3}}$

$p=-\frac{37}{12}$ and $q=\frac{431}{108}$
$\frac{p}{3}=\frac{-37}{36}$
$\frac{q}{2}=\frac{431}{216}$
$(\frac{431}{216})^2+(\frac{-37}{36})^3=\frac{139}{48}$
$t=\sqrt[3]{\frac{-431}{216}+\sqrt{\frac{139}{48}}}+\sqrt[3]{\frac{-431}{216}-\sqrt{\frac{139}{48}}}$
$t=-2.21095...$
$\therefore x=-2.21095...-\frac{5}{6}=-3.044$

We can see from the sketch below that there is only one solution and it is about $-3$ .

1 Comment

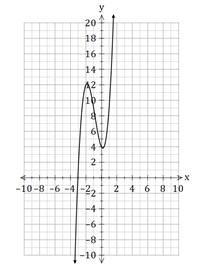
Filed under Cubics, Factorising, Polynomials, Solving

Tagged as Cardano, Cubics, Depressed Cubic, Factorising, Polynomials, Solving

Factors of Thirty	$X+Y+Z$	$XY+YZ+XZ$
$1, 1, 30$	$1+1+30=32$	$1+30+30=61$
$1, 2, 15$	$1+2+15=18$	$2+15+30=47$
$1, 5, 6$	$1+5+6=12$	$5+6+30=41$
$2, 3, 5$	$2+3+5=10$	$6+10+15=31$

Category Archives: Solving

Polynomial Long Division

Hard Equation Solving Question

Simultaneous Equation (or is it?)

Deriving the Quadratic Equation formula

Solving Cubic Functions

Recent Posts

Categories

Archives