Tag Archives: trig identities

August 14, 2025 · 6:39 am

Trig Identities and Exact Values

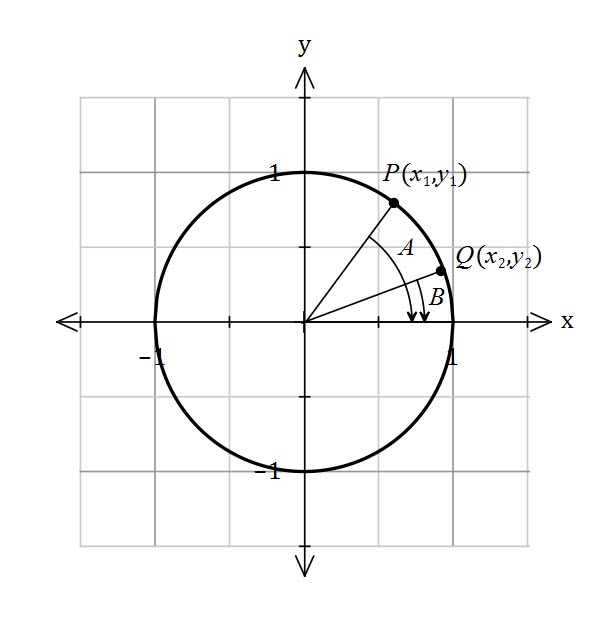
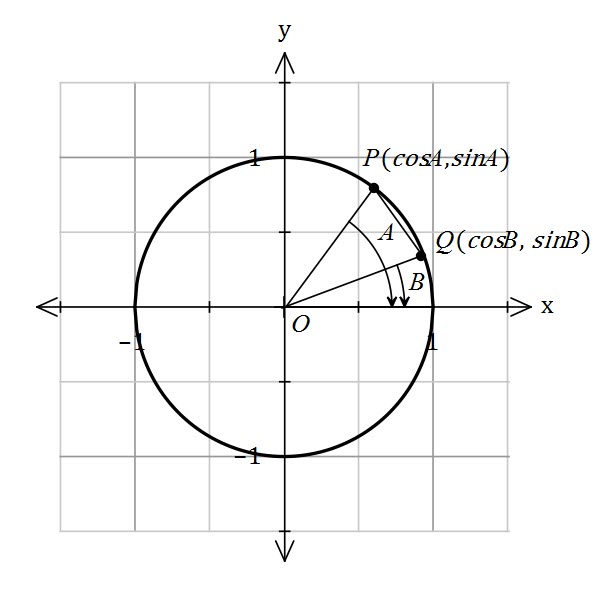
My Year 11 Specialist Mathematics students are working on Trig identities. We came across this question

Without the use of a calculator, evaluate
(a) $cos20^\circ\times cos40^\circ\times cos80^\circ$

(b) $cos(\frac{\pi}{7})\times cos(\frac{2\pi}{7})\times cos(\frac{4\pi}{7})$

OT Lee Year 11 Specialist Mathematics textbook

I spent a bit of time thinking about the question. Can you use a product to sum identity twice? But I was always being left with an angle that doesn’t have a nice exact value.

I tried a few things, had a chat to Meta AI, and finally stumbled upon this method.

Remember

$\begin{equation*}sin(2x)=2sin(x)cos(x)\end{equation}$

Which can be rearranged to

$\begin{equation*}cos(x)=\frac{sin(2x)}{sin(x)}\end{equation}$

(a) $cos20^\circ\times cos40^\circ\times cos80^\circ=\frac{sin(40)}{2sin(20)}\frac{sin(80)}{2sin(40)}\frac{sin(160)}{2sin(80)}$

Which simplifies to

$\begin{equation*}\frac{sin(160)}{8sin(20)}\end{equation}$

Now $sin(160)=sin(20)$

Hence $cos20^\circ\times cos40^\circ\times cos80^\circ=\frac{1}{8}$

And we will do the same for part (b)

$cos(\frac{\pi}{7})\times cos(\frac{2\pi}{7})\times cos(\frac{4\pi}{7})=\frac{sin(\frac{2\pi}{7})}{2sin(\frac{\pi}{7})}\frac{sin(\frac{4\pi}{7})}{2sin(\frac{2\pi}{7})}\frac{sin(\frac{8\pi}{7})}{2sin(\frac{4\pi}{7})}$

Which simplifies to

$cos(\frac{\pi}{7})\times cos(\frac{2\pi}{7})\times cos(\frac{4\pi}{7})=\frac{sin(\frac{8\pi}{7})}{8sin(\frac{\pi}{7})}$

Now $sin(\frac{8\pi}{7})=-sin(\frac{\pi}{7})$

Hence $cos(\frac{\pi}{7})\times cos(\frac{2\pi}{7})\times cos(\frac{4\pi}{7})=\frac{-1}{8}$

And then I had to test them on my Classpad.

Leave a Comment

Filed under Classpad Skills, Identities, Simplifying fractions, Trigonometry, Year 11 Specialist Mathematics

Tagged as exact values, trig identities

August 10, 2025 · 4:54 am

Trigonometric Identities – Product to Sum

Let’s think about the sine and cosine addition and subtraction trig identities.

(1) $\begin{equation*}sin(A+B)=sinAcosB+cosAsinB\end{equation*}$

(2) $\begin{equation*}sin(A-B)=sinAcosB-cosAsinB\end{equation*}$

If we add equation $1$ and $2$ , we get

$\begin{equation*}sin(A+B)+sin(A-B)=2sinAcosB\end{equation}$

Hence, $sinAcosB=\frac{1}{2}(sin(A+B)+sin(A-B))$

If we subtract equation $2$ from equation $1$ , we get

$\begin{equation*}sin(A+B)-sin(A-B)=2cosAsinB\end{equation}$

Hence, $cosAsinB=\frac{1}{2}(sin(A+B)-sin(A-B)$

What about the cosine addition and subtraction idenities?

(3) $\begin{equation*}cos(A+B)=cosAcosB-sinAsinB\end{equation*}$

(4) $\begin{equation*}cos(A-B)=cosAcosB+sinAsinB\end{equation*}$

If we add equation $3$ and $4$ , we get

$\begin{equation*}cos(A+B)+cos(A-B)=2cosAcosB\end{equation}$

Hence, $cosAcosB=\frac{1}{2}(cos(A+B)+cos(A-B))$

If we subtract $3$ from $4$ , we get

$\begin{equation*}cos(A-B)-cos(A+B)=2sinAsinB\end{equation}$

Hence, $sinAsinB=\frac{1}{2}(cos(A-B)-cos(A+B))$

These are the product to sum identities.

$\begin{equation*}sinAcosB=\frac{1}{2}(sin(A+B)+sin(A-B))\end{equation}$

$\begin{equation*}cosAsinB=\frac{1}{2}(sin(A+B)-sin(A-B))\end{equation}$

$\begin{equation*}cosAcosB=\frac{1}{2}(cos(A+B)+cos(A-B))\end{equation}$

$\begin{equation*}sinAsinB=\frac{1}{2}(cos(A-B)-cos(A+B))\end{equation}$

Examples

(1) Solve $sin(5x)-sin(x)=0$ for $0\le x \le 2\pi$

Remember,

$\begin{equation*}cosAsinB=\frac{1}{2}(sin(A+B)-sin(A-B))\end{equation}$

$\begin{equation*}A+B=5\end{equation}$

$\begin{equation*}A-B=1\end{equation}$

Therefore, $A=3$ and $B=2$

$\begin{equation*}sin(5x)-sin(x)=2cos(3x)sin(2x)=0\end{equation}$

$\begin{equation*}cos(3x)=0\end{equation}$

$\begin{equation*}3x=\frac{\pi}{2},\frac{3\pi}{2}, \frac{5\pi}{2}, \frac{7\pi}{2}, \frac{\9\pi}{2}, \frac{11\pi}{2}\end{equation}$

$\begin{equation*}x=\frac{\pi}{6}, \frac{\pi}{2}, \frac{5\pi}{6}, \frac{7\pi}{6}, \frac{3\pi}{2}, \frac{11\pi}{6}\end{equation}$

$\begin{equation*}sin(2x)=0\end{equation}$

$\begin{equation*}2x=0, \pi, 2\pi, 3\pi, 4\pi\end{equation}$

$\begin{equation*}x=0, \frac{\pi}{2}, \pi, \frac{3\pi}{2}, 2\pi\end{equation}$

Hence $x=0, \frac{\pi}{6}. \frac{\pi}{2}, \frac{5\pi}{6}, \pi, \frac{7\pi}{6}, \frac{3\pi}{2}, \frac{11\pi}{6}, 2\pi$

(2)Solve $sin(7\theta)-sin(\theta)=sin(3\theta)$ for $0 \le \theta \le\2\pi$

$\begin{equation*}cosAsinB=\frac{1}{2}(sin(A+B)-sin(A-B))\end{equation}$

Therefore, $A+B=7$ and $A-B=1$

$A=4, B=3$

$\begin{equation*}2cos(4\theta)sin(3\theta)=sin(3\theta)\end{equation}$

$\begin{equation*}2cos(4\theta)sin(3\theta)-sin(3\theta)=0\end{equation}$

$\begin{equation*}sin(3\theta)(2cos(4\theta)-1)=0\end{equation}$

$sin(3\theta)=0$ and $cos(4\theta)=\frac{1}{2}$

$3\theta=0, \pi, 2\pi, 3\pi, 4\pi, 5\pi, 6\pi$

$\theta=0, \frac{\pi}{3}, \frac{2\pi}{3}, \frac{4\pi}{3}, \frac{5\pi}{3}. 2\pi$

$cos(4\theta)=\frac{1}{2}$

$4\theta=\frac{\pi}{3}, \frac{5\pi}{3}, \frac{7\pi}{3}, \frac{11\pi}{3}, \frac{13\pi}{3}, \frac{17\pi}{3}, \frac{19\pi}{3}, \frac{23\pi}{3}$

$\theta=\frac{\pi}{12}, \frac{5\pi}{12}, \frac{7\pi}{12}, \frac{11\pi}{12}, \frac{13\pi}{12}, \frac{17\pi}{12}, \frac{19\pi}{12}, \frac{23\pi}{12}$

Hence $\theta=0, \frac{\pi}{3}, \frac{5\pi}{12}, \frac{7\pi}{12}, \frac{11\pi}{12}, \frac{13\pi}{12}, \frac{17\pi}{12}, \frac{5\pi}{3}, \frac{23\pi}{12}, 2\pi$

Leave a Comment

Filed under Addition and Subtraction Identities, Identities, Product to Sum idenitites, Trigonometry

Tagged as product to sum trig identities, solving trig equations, trig identities

July 28, 2025 · 8:09 am

Trig Identities – Addition and Subtraction

Deriving the addition and subtraction trigonometric identities.

We will start with cosine, and use the result to derive the remaining identities.

Proving $cos(A-B)=cos(A)cos(B)+sin(A)(sin(B)$ .

$A$ and $B$ are represented in the unit circle below.

Remember $P(x_1,y_1)=(cos(A), sin(A))$ and $Q(x_2, y_2)=(cos(B), sin(B))$

Using the cosine rule and triangle $OPQ$ , find $PQ$

$\begin{equation*}(PQ)^2=1^2+1^2-2(1)(1)cos(A-B)\end{equation}$

$\begin{equation*}(PQ)^2=2-2cos(A-B)\end{equation}$

Using the distance between points, find $PQ$

$\begin{equation*}(PQ)^2=(x_1-x_2)^2+(y_1-y_2)^2\end{equation}$

$\begin{equation*}(PQ)^2=(cosA-cosB)^2+(sinA-sinB)^2\end{equation}$

$(PQ)^2=cos^2A-2cosAcosB+cos^2B+sin^2A-2sinAsinB+sin^2B$

Remember the Pythagorean identity

$\begin{equation*}cos^2\theta+sin^2\theta=1\end{equation}$

$\begin{equation*}(PQ)^2=2-2cosAcosB-2sinAsinB\end{equation}$

Hence

$\begin{equation*}2-2cos(A-B)=2-2cosAcosB-2sinAsinB\end{equation}$

(1) $\begin{equation*}cos(A-B)=cosAcosB+sinAsinB\end{equation*}$

We can then use this identity to find $cos(A+B)$ .

$\begin{equation*}cos(A+B)=cos(A-(-B))\end{equation}$

$\begin{equation*}cos(A-(-B))=cos(A)cos(-B)+sinAsin(-B)\end{equation}$

Remember $cos(-B)=cos(B)$ and $sin(-B)=-sin(B)$

$\begin{equation*}cos(A-(-B))=cosAcosB-sinAsinB\end{equation}$

(2) $\begin{equation*}cos(A+B)=cosAcosB-sinAsinB\end{equation*}$

We can also find $sin(A+B)$

Remember, $sin\theta=cos(\frac{\pi}{2}-\theta)$

$\begin{equation*}sin(A+B)=cos(\frac{\pi}{2}-(A+B))\end{equation}$

$\begin{equation*}sin(A+B)=cos((\frac{\pi}{2}-A)-B)\end{equation}$

$\begin{equation*}sin(A+B)=cos(\frac{\pi}{2}-A)cosB+sin(\frac{\pi}{2}-A)sinB\end{equation}$

(3) $\begin{equation*}sin(A+B)=sinAcosB+cosAsinB\end{equation*}$

We can use equation $2$ to find $sin(A-B)$

$\begin{equation*}sin(A-B)=sin(A+(-B))\end{equation}$

$\begin{equation*}sin(A+(-B))=sinAcos(-B)+cosAsin(-B)\end{equation}$

$\begin{equation*}sin(A+(-B))=sinAcos(B)-cosAsin(B)\end{equation}$

(4) $\begin{equation*}sin(A-B)=sinAcos(B)-cosAsin(B)\end{equation*}$

And we can use both the sine and cosine identities to find $tan(A+B)$

Remember $tan\theta=\frac{sin\theta}{cos\theta}$

$\begin{equation*}tan(A+B)=\frac{sin(A+B)}{cos(A+B)}\end{equation}$

$\begin{equation*}=\frac{sinAcosB+cosAsinB}{cosAcosB-sinAsinB}\end{equation}$

$\begin{equation*}=\frac{sinAcosB+cosAsinB}{cosAcosB-sinAsinB}\times \frac{cosAcosB}{cosAcosB}\end{equation}$

$\begin{equation*}=\frac{\frac{sinAcosB}{cosAcosB}+\frac{cosAsinB}{cosAcosB}}{\frac{cosAcosB}{cosAcosB}+\frac{sinAsinB}{cosAcosB}}\end{equation}$

$\begin{equation*}=\frac{tanA+tanB}{1-tanAtanB}\end{equation}$

(5) $\begin{equation*}tan(A+B)=\frac{tanA+tanB}{1-tanAtanB}\end{equation*}$

and

(6) $\begin{equation*}tan(A-B)=\frac{tanA-tanB}{1+tanAtanB}\end{equation*}$

$\begin{equation*}cos(A\pm B)=cosAcosB\mp sinAsinB\end{equation}$

$\begin{equation*}sin(A\pm B)=sinAcosB\pm cosAsinB\end{equation}$

$\begin{equation*}tan(A \pm B)=\frac{tan A \pm tanB}{1 \mp tanAtanB}\end{equation}$

Leave a Comment

Filed under Addition and Subtraction Identities, Identities, Non-Right Trigonometry, Simplifying fractions, Trigonometry, Year 11 Mathematical Methods, Year 11 Specialist Mathematics

Tagged as addition and subtraction trig identities, trig identities

February 3, 2025 · 9:11 am

Differentiating Trigonometric Functions

In the last post we looked at two trig limits:

(1) $\begin{equation*}\lim_{x \to 0}\frac{sin(x)}{x}=1\end{equation*}$

(2) $\begin{equation*}\lim_{x \to 0}\frac{1-cos(x)}{x}=0\end{equation*}$

We are going to use these two limits to differentiate sine and cosine functions from first principals.

$\begin{equation*}f(x)=sin(x)\end{equation}$

$\begin{equation*}f'(x)=\lim\limits_{h \to 0}\frac{sin(x+h)-sin(x)}{h}\end{equation}$

Use the trig identity

$\begin{equation*}sin(A+B)=sinAcosB+sinBcosA\end{equation}$

$\begin{equation*}f'(x)=\lim\limits_{h \to 0}\frac{sin(x)cos(h)+sin(h)cos(x)-sin(x)}{h}\end{equation}$

$\begin{equation*}f'(x)=\lim\limits_{h \to 0}(\frac{sin(x)(cos(h)-1)}{h}+\frac{sin(h)cos(x)}{h})\end{equation}$

$\begin{equation*}f'(x)=sin(x)\lim\limits_{h \to 0}(\frac{(cos(h)-1)}{h}+cos(x)\lim\limits_{h \to 0}\frac{sin(h)}{h}\end{equation}$

$\begin{equation*}f'(x)=sin(x)\lim\limits_{h \to 0}(\frac{-(-cos(h)+1)}{h}+cos(x)\lim\limits_{h \to 0}\frac{sin(h)}{h}\end{equation}$

Evaluate the limits

$\begin{equation*}f'(x)=sin(x)\times 0+cos(x)\times (1)=cos(x)\end{equation}$

Hence, $\frac{d}{dx}sin(x)=cos(x)$ .

Now we are going to do the same for $f(x)=cos(x)$ .

$\begin{equation*}f'(x)=\lim\limits_{h \to 0}\frac{cos(x+h)-cos(x)}{h}\end{equation}$

Use the trigonometric identity

$\begin{equation*}cos(A+B)=cosAcosB-sinAsinB\end{equation}$

$\begin{equation*}f'(x)=\lim\limits_{h \to 0}\frac{cos(x)cos(h)-sin(x)sin(h)-cos(x)}{h}\end{equation}$

$\begin{equation*}f'(x)=\lim\limits_{h \to 0}\frac{cos(x)(cos(h)-1)-sin(x)sin(h)}{h}\end{equation}$

$\begin{equation*}f'(x)=cos(x)\lim\limits_{h \to 0}\frac{-(1-cos(h))}{h}-sin(x)\lim\limits_{h \to 0}\frac{sin(h)}{h}\end{equation}$

Evaluate the limits

$\begin{equation*}f'(x)=cos(x)\times(0)-sin(x)\times (1)=-sin(x)\end{equation}$

Hence $\frac{d}{dx} cos(x)=-sin(x)$

1 Comment

Filed under Calculus, Differentiation, Identities, Trigonometry, Year 12 Mathematical Methods

Tagged as differentiation, trig differentiation, trig identities, trig limits, trigonometric differentiation, trigonometric identities, trigonometric limits

October 1, 2024 · 7:31 am

Using De Moivre’s Theorem for Trigonometric Identities

We are going to use De Moivre’s theorem to prove trigonometric identities.

Remember, De Moivre’s Theorem

If $z=r(cos(\theta)+isin(\theta))$ , then $z^n=r^n(cos(n\theta)+isin(n\theta))$

Or a shorter version $z=rcis(\theta)$ , then $z^n=r^ncis(n\theta)$

Now, let $z=cos(\theta)+isin(\theta)$ , find $z+\frac{1}{z}$

$z+z^{-1}=cos(\theta)+isin(\theta)+cos(-\theta)+isin(-\theta)$

Remember $cos(\theta)=cos(\theta)$ and $sin(-\theta)=-sin(\theta)$

$z+\frac{1}{z}=cos(\theta)+isin(\theta)+cos(\theta)-isin(\theta)$

$z+\frac{1}{z}=2cos(\theta)$

It is the same for $z^n+\frac{1}{z^n}$

$z^n+z^{-n}=cos(n\theta)+isin(n\theta)+cos(-n\theta)+isin(-n\theta)$

$z^n+\frac{1}{z^n}=2cos(n\theta)$

We can do something similar with sine.

$z-\frac{1}{z}=cos(\theta)+isin(\theta)-(cos(-\theta)+isin(-\theta))$

$z-\frac{1}{z}=cos(\theta)+isin(\theta)-(cos(\theta)-isin(\theta))$

$z-\frac{1}{z}=cos(\theta)+isin(\theta)-cos(\theta)+isin(\theta)$

$z-\frac{1}{z}=2isin(\theta)$

Hence $z^n-\frac{1}{z^n}=2isin(n\theta)$

Let’s find an identity for $cos(3\theta)$

$cos(3\theta)=\frac{1}{2}(z^3+\frac{1}{z^3})$

$=\frac{1}{2}(z^3+\frac{1}{z^3}+3z^2\times\frac{1}{z}+3z\times\frac{1}{z^2}-3z^2\times\frac{1}{z}-3z\times\frac{1}{z^2})$

$=\frac{1}{2}((z+\frac{1}{z})^3-3z-\frac{3}{z})$

$=\frac{1}{2}((z+\frac{1}{z})^3-3(z+\frac{1}{z}))$

$=\frac{1}{2}(2cos(\theta))^3-3(2cos(\theta)))$

$=\frac{1}{2}(8cos^3(\theta)-6cos(\theta))$

$=4cos^3(\theta)-3cos(\theta)$

$\therefore cos(3\theta)=4cos^3(\theta)-3cos(\theta)$

And $sin(3\theta)$ ?

$sin(3\theta)=\frac{1}{2i}(z^3-\frac{1}{z^3})$

$=\frac{1}{2i}(z^3-\frac{1}{z^3}-3z^2\times\frac{1}{z}+3z\times\frac{1}{z^2}+3z^2\times\frac{1}{z}-3z\times\frac{1}{z^2}$

$=\frac{1}{2i}((z-\frac{1}{z})^3+3z-\frac{3}{z})$

$=\frac{1}{2i}(2isin(\theta))^3+3(z-\frac{1}{z}))$

$=\frac{1}{2i}(-8isin^3(\theta)+6isin(\theta))$

$=-4sin^3(\theta)+3sin(\theta)$

$\therefore sin(3\theta)=3sin(\theta)-4sin^3(\theta)$

Leave a Comment

Filed under Complex Numbers, Identities, Trig Identities, Trigonometry

Tagged as complex numbers, de moivre, trig identities

Tag Archives: trig identities

Trig Identities and Exact Values

Trigonometric Identities – Product to Sum

Examples

Trig Identities – Addition and Subtraction

Differentiating Trigonometric Functions

Using De Moivre’s Theorem for Trigonometric Identities

Recent Posts

Categories

Archives