counting techniques

Tag Archives: counting techniques

May 28, 2025 · 1:33 pm

A Counting Question

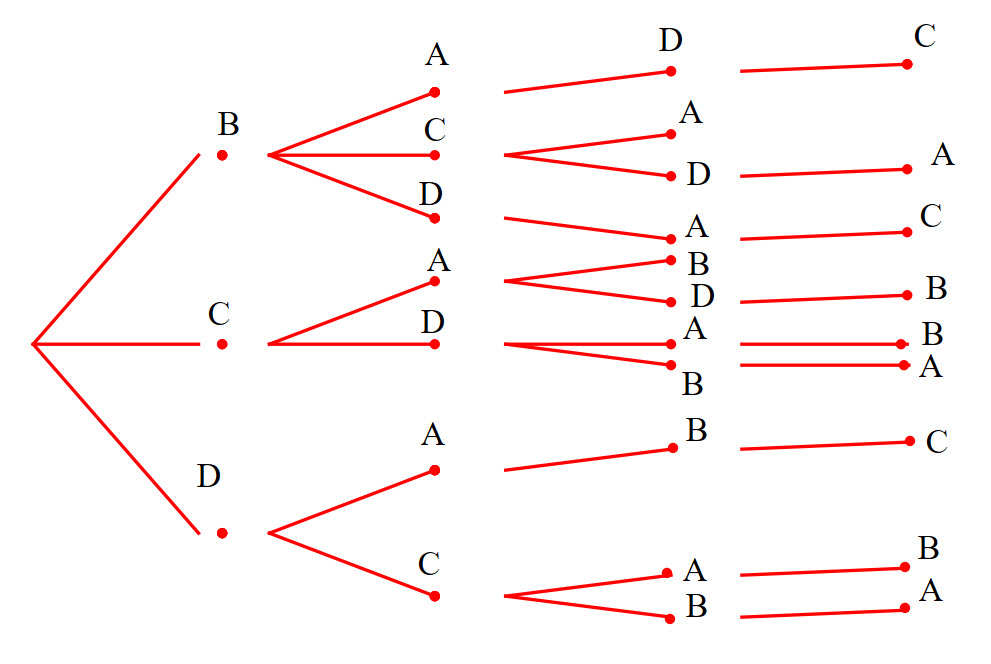
How many three digit numbers can you form from the digits 1, 2, 3, 4 and 5 if

(a) the digits must occur in increasing order?

(b) adjacent digits differ by 2?

Cambridge Year 11 Specialist Mathematics Skill Sheet 1A

(a) There are $5\times 4\times 3=60$ permutations of three digits from the five digits, but how many of those are in the right order?

Each set of 3 digits has 6 arrangements ( $3\times 2\times 1=6$ ).

For example, if the set is ${1, 2, 3}$ , then the possible arrangements are:

123, 132, 213, 231, 312, and 321.

Only one of those arrangements is in numerical order.

Hence what we want is $\begin{pmatrix}5\\3\end{pmatrix}=10$

(b) I think this one is more about creating a list. I shall start with 1

135, 531, 131, 242, 353, 424, 535, 315

There are 8 possibilities.

Four teachers decide to swap desks at work. How many ways can this be done if no teacher sits at their previous desk?
Mathematics Specialist Units 1&2 Cambridge

I like this question as it seems easy until you start thinking about it. I think the best approach is a tree diagram.

If we think of the four teachers as A, B, C and D. Then A can no longer sit in A, so the options are B, C and D for the first desk.

For the second desk, If B is in the first desk, then A, C or D could be in the second. If C is in the first desk, then A or D could be in the second (B can’t be in the same desk). If D is in the first desk, then A or C can be in the second desk.

Tag Archives: counting techniques

A Counting Question

Counting Techniques

Recent Posts

Categories

Archives