circle theorems | Racquel Sanderson

Tag Archives: circle theorems

November 16, 2025 · 5:54 am

Geometry Circle Question

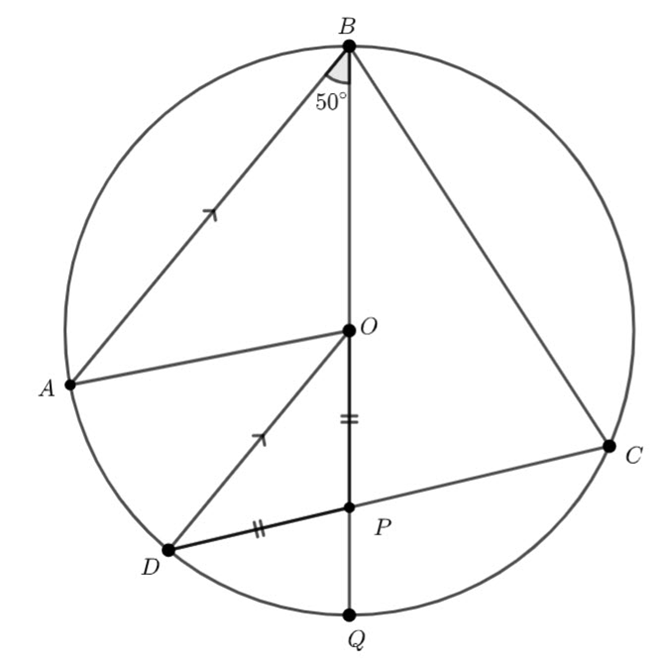
In the diagram below, $A, B, C$ and $D$ lie on the circle with centre $O$ . If $\angle{DBC} = 41^{\circ}$ and $\angle{ACD} = 53^{\circ}$ , determine with reasoning $\angle{BAC}$ and $\angle{AOB}$

We know $OA=OB=OD$ – radii of the circle.

Which means, $\Delta{AOB}$ is isosceles and $\angle{OAB}=\angle{OBA}$ – equal angles isosceles triangle.

$\angle{AOD}=2\angle{ACD}$ – angle at the centre twice the angle at the circumference.

$\angle{AOB}=106^{\circ}$

This means $\angle{AOB}=74^{\circ}$ – angles on a straight line are supplementary

$\angle{OAD}=\angle{ODA}=37^{\circ}$ – equal angles isosceles triangle and the angle sum of a triangle.

$\angle{DBA}=\angle{DCA}=53^{\circ}$ – angle at the circumference subtended by the same arc are congruent.

$\angle{CAD}=\angle{CBD}=41^{\circ}$ – angles at the circumference subtended by the same arc are congruent.

$\angle{OAB}=53^{\circ}$ – equal angle isosceles triangle

Hence $\angle{BAC}=12^{\circ}$

In the diagram, points $A, B, C, D$ and $Q$ lie on a circle centre $O$ , radius $6$ cm and diameter $BQ, \angle{ABQ}=50^\circ, AB$ is parallel to $DO$ and point $P$ lies on diameter $BQ$ such that $OP=DP=4$ cm.

(a) Find $\angle{BCD}$

(b) Determine the length of $PC$ .

$\angle{BOD}=180^\circ-50^\circ=130^\circ$ (Co-interior angles in parallel lines are supplementary.)

$\angle{BCD}=\frac{1}{2}\times 130=65^\circ$ (Angles subtended by the same arc. The angle at the centre is twice the angle at the circumference.)

$\angle{BCD}=65^\circ.$

Let $PC=x$

From the intersecting chord theorem

$\begin{equation*}4\times x=2\times 10\end{equation}$

$\begin{equation*}4x=20\end{equation}$

$\begin{equation*}x=5\end{equation}$

$PC=5cm$

A chord $AB$ of a circle $O$ is extended to $C$ . The straight line bisecting $\angle{OAB}$ meets the circle at $E$ . Let $\angle{BAE}=x$ . Prove that $EB$ bisects $\angle{OBC}$ .