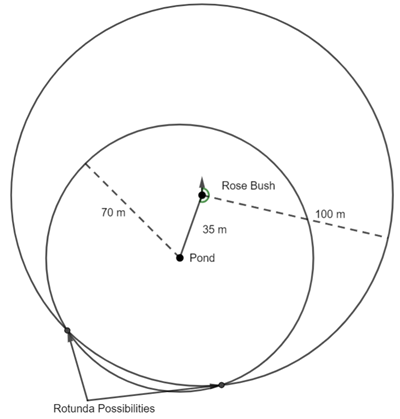
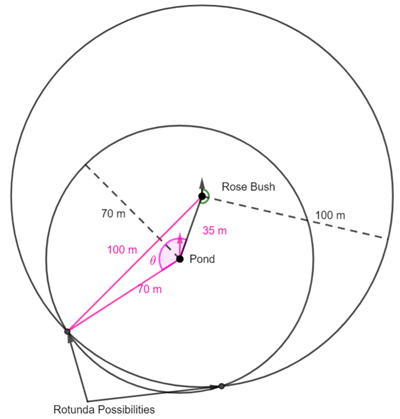
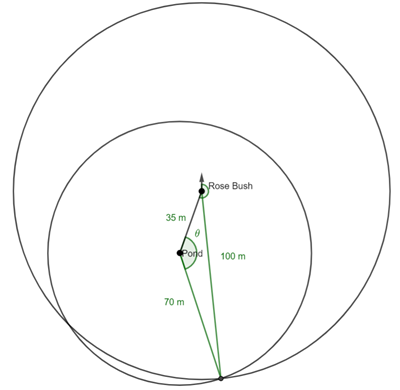
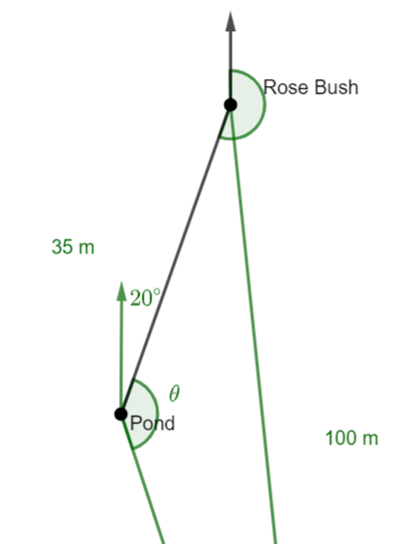
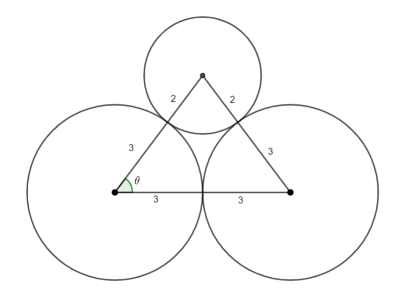
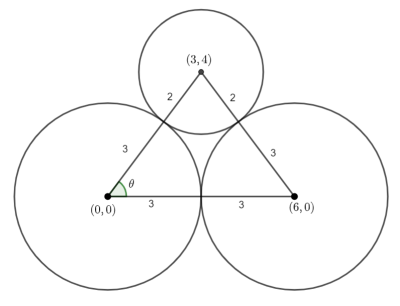
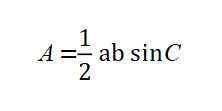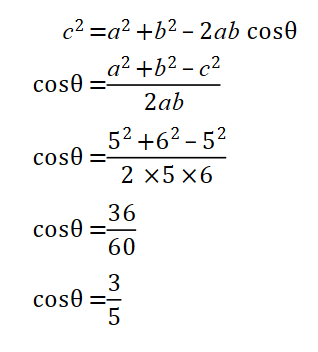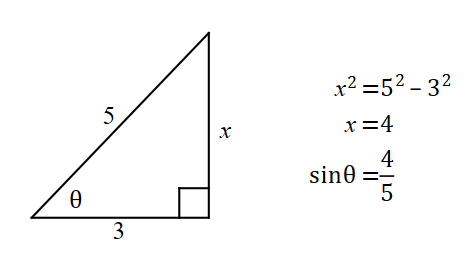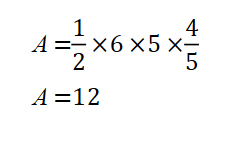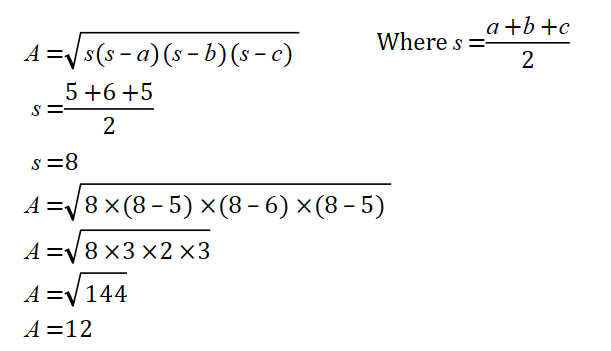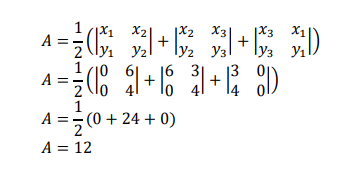This is question 5 from the UK Maths Trust Senior Challenge October 2023.
I have tackled this in three ways; using non-right trig to find the area, Heron’s Law, and the Shoelace Formula.
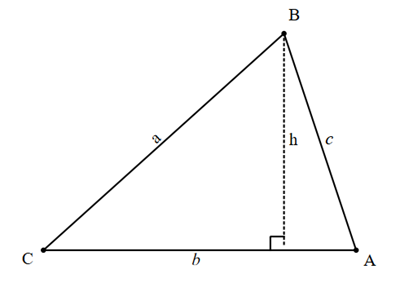
Method 1
Use the area of a triangle formula
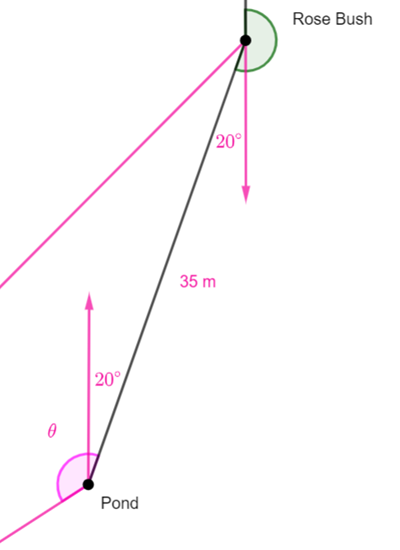
Use the cosine rule to find cosθ.
Once we have cosθ, we can find sinθ.
Hence the area is,
Method 2
Use Heron’s law.
Heron’s law is a way of calculating area of a triangle from the lengths of the three sides of the triangle.
This is my preferred method – simple and direct.
Method 3
Shoelace formula (Gauss’s Area formula)
We need to allocate each of the vertices a co-ordinate.
The co-ordinates are listed in an anti-clockwise direction.
This is probably a bit over the top, but once you get the hang of it, it’s very easy.
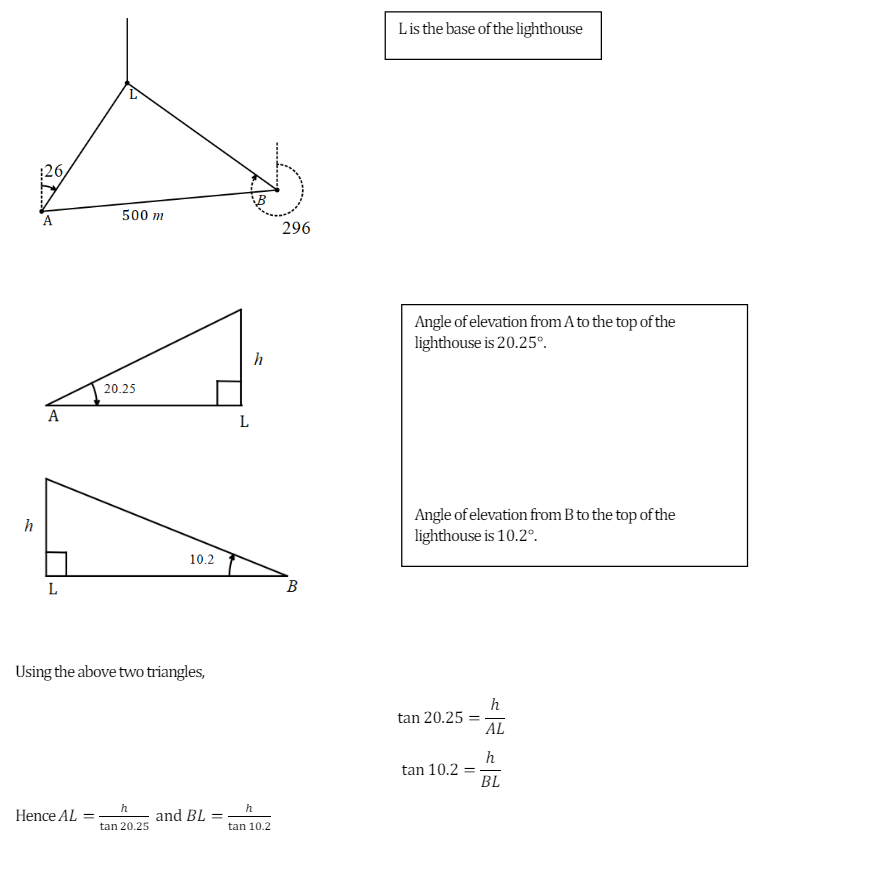
![]() , then
, then ![]()
![]() , then
, then ![]()
![]() , find
, find ![]()
![]()
![]() and
and ![]()
![]()
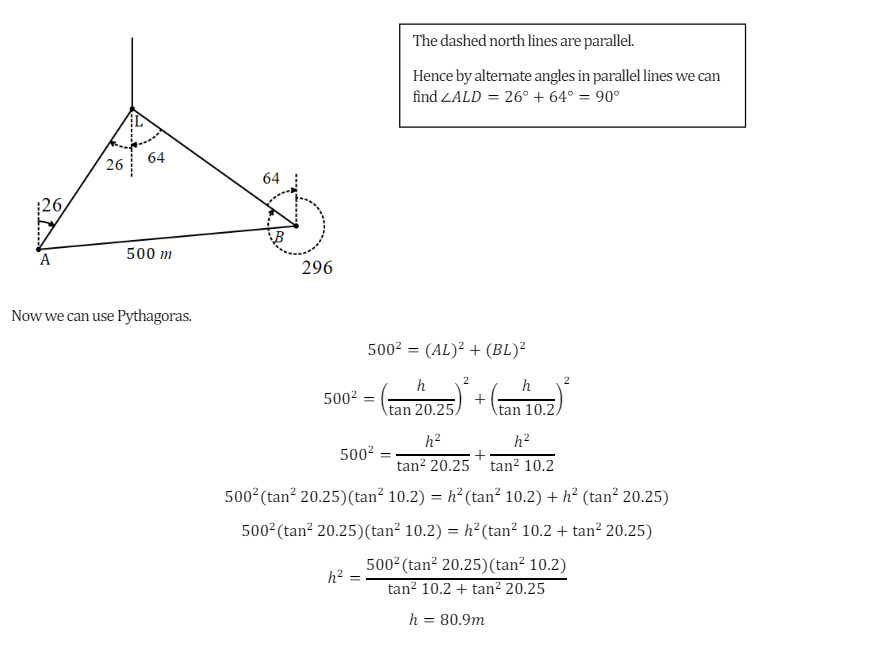
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ?
?![]()
![]()
![]()
![]()
![]()
![]()
![]()