Category Archives: Identities

February 2, 2025 · 7:46 am

Trigonometric Limits

$\lim\limits_{x \to 0}\frac{sin(x)}{x}=?$

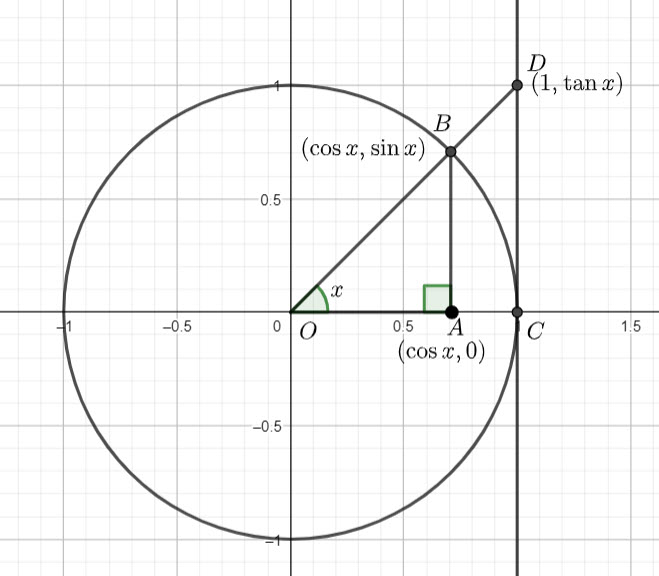
Remember $cos(x)=\frac{OA}{OB}=\frac{OA}{1}$ , hence $OA=cos(x)$ and the co-ordinate of $A$ is $(cos(x), 0)$ .

$sin(x)=\frac{AB}{OB}=\frac{AB}{1}$ , hence $AB=sin(x)$ and the co-ordinate of $B$ is $(cos(x), sin(x))$

And from the definition of $tan(x)$ we know $D$ is the point $(1, tan(x))$

Consider the areas of triangle $OAB$ , sector $OBC$ , and triangle $OCD$ .

We know from inspection of the above diagram that

Area $OAB<$ Area $OCB<$ Area $OCD$

Which means,

$\frac{1}{2}b_1 h_1<\frac{1}{2}r^2x<\frac{1}{2}b_2 h_2$

We can ignore all of the halves.

$cos(x)sin(x)<x<(1)tan(x)$

Remember $tan(x)=\frac{sin(x)}{cos(x)}$

$cos(x)sin(x)<x<\frac{sin(x)}{cos(x)}$

Divide everything by $sin(x)$ (as we are in the first quadrant we know $sin(x)>0$ , so we don’t need to worry about the inequality)

$cos(x)<\frac{x}{sin(x)}<\frac{1}{cos(x)}$

Invert everything and change the direction of the inequalities)

$\frac{1}{cos(x)}>\frac{sin(x)}{x}>cos(x)$

I am going to rewrite it as follows

$cos(x)<\frac{sin(x)}{x}<\frac{1}{cos(x)}$

because I like to use less thans rather than greater thans.

Now what happens as $x$ tends to $0$ ?

$cos(0)=1$

$1<\frac{sin(x)}{x}<\frac{1}{1}$

Hence by the squeeze theorem $\lim\limits_{x \to 0}\frac{sin(x)}{x}=1$

Now we know this limit, we are going to use it to find $\lim\limits_{x \to 0}\frac{1-cos(x)}{x}$

Multiply by $\frac{1+cos(x)}{1+cos(x)}$

$\lim\limits_{x \to 0}\frac{1-cos(x)}{x}\times \frac{1+cos(x)}{1+cos(x)}$

$\lim\limits_{x \to 0}\frac{1-cos^2(x)}{x(cos(x)+1)}$

$\lim\limits_{x \to 0}\frac{sin^2(x)}{x(cos(x)+1)}$

$\lim\limits_{x \to 0}\frac{sin(x)}{x}\times sin(x)(cos(x)+1)}$

$\lim\limits_{x \to 0}\frac{sin(x)}{x}\times \lim\limits_{x \to 0}sin(x)(cos(x)+1)$

If we evaluate the limits,

$(1)(sin(0)(cos(0)+1)=1\times 0 \times 2=0$

Hence, $\lim\limits_{x \to 0}\frac{1-cos(x)}{x}=0$

In the next post we are going to use these limits to differentiate sine and cosine functions.

1 Comment

Filed under Area, Area of Triangles (Sine), Calculus, Identities, Trigonometry, Year 12 Mathematical Methods

Tagged as trig limits, trigonometric limits

December 16, 2024 · 9:19 am

Interesting Sum

$S=\sum_{n=1}^\infty (tan^{-1}(\frac{2}{n^2}))$ , find $S$ .

I came across this sum in An Imaginary Tale by Nahin and I was fascinated.

Let $tan(\alpha)=n+1$ and $tan(\beta)=n-1$ .

tan(\alpha-\beta)=\frac{tan(\alpha)-tan(\beta)}{1+tan(\alpha)tan(\beta)}

tan(\alpha-\beta)=\frac{(n+1)-(n-1)}{1+(n+1)(n-1)}

Which means,

$\begin{equation*}S=\sum_{n=1}^\infty(tan^{-1}(n+1)-tan^{-1}(n-1))\end{equation}$

Let’s try a few partial sums

$S_4=tan^{-1}(2)-tan^{-1}(0)+tan^{-1}(3)-tan^{-1}(1)+tan^{-1}(4)-tan^{-1}(2)+tan^{-1}(5)-tan^{-1}(3)$

$S_4=-tan^{-1}(0)+-tan^{-1}(1)+tan^{-1}(4)+tan^{-1}(5)$

$S_6=tan^{-1}(2)-tan^{-1}(0)+tan^{-1}(3)-tan^{-1}(1)+tan^{-1}(4)-tan^{-1}(2)+tan^{-1}(5)-tan^{-1}(3)+tan^{-1}(6)-tan^{-1}(4)+tan^{-1}(7)-tan^{-1}(5)$

$S_6=-tan^{-1}(0)+-tan^{-1}(1)+tan^{-1}(6)+tan^{-1}(7)$

Hence, $S_N=-tan^{-1}(0)+-tan^{-1}(1)+tan^{-1}(N)+tan^{-1}(N+1)$

$S_N=-\frac{\pi}{4}-0+tan^{-1}(N)+tan^{-1}(N+1)$

What happens as $N\rightarrow \infty$ ?

$\lim\limits_{N\to \infty}\ S_N=-\frac{\pi}{4}+\frac{\pi}{2}+\frac{\pi}{2}=\frac{3\pi}{4}$

Because we know $tan(\frac{\pi}{2})$ is undefined.

1 Comment

Filed under Identities, Interesting Mathematics, Puzzles, Sequences, Trigonometry

Tagged as limits, sum, trigonometric identities

November 26, 2024 · 7:07 am

Infinite Product Expansion of cos (x)

Remember

(1) $\begin{equation*}cos(x)=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+...\end{equation*}$

We know that $cos(x)=0$ for odd integer multiples of $\frac{\pi}{2}$ , i.e. $\frac{\pi}{2}, \frac{3\pi}{2}, ...$ , which is $\frac{(2n-1)\pi}{2}$ for $n\neq 0$

Hence,

$\begin{equation*}0=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+...\end{equation}$

for $x=\frac{(2n-1)\pi}{2}, n>0$

We can factorise our $cos(x)$ expansion

$\begin{equation*}(1-\frac{x^2}{r_1})(1-\frac{x^2}{r_2})...\end{equation}$

We know $r_1=\frac{\pi}{2}, r_2=\frac{3\pi}{2}, ...$

$\begin{equation*}cos(x)=(1-\frac{x^2}{(\frac{\pi}{2})^2})(1-\frac{x^2}{(\frac{3\pi}{2})^2})...(1-\frac{x^2}{(\frac{(2n-1)\pi}{2})^2})\end{equation}$

$\begin{equation*}cos(x)=\Pi_{n=1}^{\infty}(1-\frac{x^2}{(\frac{(2n-1)\pi}{2})^2})\end{equation}$

$\begin{equation*}cos(x)=\Pi_{n=1}^{\infty}(1-\frac{4x^2}{(2n-1)^2\pi^2})\end{equation}$

1 Comment

Filed under Factorising, Identities, Infinite Product Expansion, Interesting Mathematics, Polynomials, Trigonometry

Tagged as infinite product expansion of cos(x), trigonometry

October 1, 2024 · 7:31 am

Using De Moivre’s Theorem for Trigonometric Identities

We are going to use De Moivre’s theorem to prove trigonometric identities.

Remember, De Moivre’s Theorem

If $z=r(cos(\theta)+isin(\theta))$ , then $z^n=r^n(cos(n\theta)+isin(n\theta))$

Or a shorter version $z=rcis(\theta)$ , then $z^n=r^ncis(n\theta)$

Now, let $z=cos(\theta)+isin(\theta)$ , find $z+\frac{1}{z}$

$z+z^{-1}=cos(\theta)+isin(\theta)+cos(-\theta)+isin(-\theta)$

Remember $cos(\theta)=cos(\theta)$ and $sin(-\theta)=-sin(\theta)$

$z+\frac{1}{z}=cos(\theta)+isin(\theta)+cos(\theta)-isin(\theta)$

$z+\frac{1}{z}=2cos(\theta)$

It is the same for $z^n+\frac{1}{z^n}$

$z^n+z^{-n}=cos(n\theta)+isin(n\theta)+cos(-n\theta)+isin(-n\theta)$

$z^n+\frac{1}{z^n}=2cos(n\theta)$

We can do something similar with sine.

$z-\frac{1}{z}=cos(\theta)+isin(\theta)-(cos(-\theta)+isin(-\theta))$

$z-\frac{1}{z}=cos(\theta)+isin(\theta)-(cos(\theta)-isin(\theta))$

$z-\frac{1}{z}=cos(\theta)+isin(\theta)-cos(\theta)+isin(\theta)$

$z-\frac{1}{z}=2isin(\theta)$

Hence $z^n-\frac{1}{z^n}=2isin(n\theta)$

Let’s find an identity for $cos(3\theta)$

$cos(3\theta)=\frac{1}{2}(z^3+\frac{1}{z^3})$

$=\frac{1}{2}(z^3+\frac{1}{z^3}+3z^2\times\frac{1}{z}+3z\times\frac{1}{z^2}-3z^2\times\frac{1}{z}-3z\times\frac{1}{z^2})$

$=\frac{1}{2}((z+\frac{1}{z})^3-3z-\frac{3}{z})$

$=\frac{1}{2}((z+\frac{1}{z})^3-3(z+\frac{1}{z}))$

$=\frac{1}{2}(2cos(\theta))^3-3(2cos(\theta)))$

$=\frac{1}{2}(8cos^3(\theta)-6cos(\theta))$

$=4cos^3(\theta)-3cos(\theta)$

$\therefore cos(3\theta)=4cos^3(\theta)-3cos(\theta)$

And $sin(3\theta)$ ?

$sin(3\theta)=\frac{1}{2i}(z^3-\frac{1}{z^3})$

$=\frac{1}{2i}(z^3-\frac{1}{z^3}-3z^2\times\frac{1}{z}+3z\times\frac{1}{z^2}+3z^2\times\frac{1}{z}-3z\times\frac{1}{z^2}$

$=\frac{1}{2i}((z-\frac{1}{z})^3+3z-\frac{3}{z})$

$=\frac{1}{2i}(2isin(\theta))^3+3(z-\frac{1}{z}))$

$=\frac{1}{2i}(-8isin^3(\theta)+6isin(\theta))$

$=-4sin^3(\theta)+3sin(\theta)$

$\therefore sin(3\theta)=3sin(\theta)-4sin^3(\theta)$

Category Archives: Identities

Trigonometric Limits

Interesting Sum

Infinite Product Expansion of cos (x)

Using De Moivre’s Theorem for Trigonometric Identities

Recent Posts

Categories

Archives