Category Archives: Cubics

November 22, 2025 · 6:10 am

Polynomial Long Division

I usually choose to use synthetic division when factorising polynomials, but I know some teachers are unhappy when their students do this. So for completeness, here is my PDF for Polynomial Long Division.

Polynomial Long DivisionDownload

Leave a Comment

Filed under Algebra, Cubics, Factorisation, Factorising, Factorising, Polynomials, Quadratics, Solving, Solving, Solving Equations, Year 11 Mathematical Methods

Tagged as ,

July 11, 2025 · 5:35 am

Simultaneous Equation (or is it?)

Solve simultaneously

X+Y+Z=10
XYZ=30
XY+YZ+XZ=31

We could attempt to solve this simultaneously, but I think the algebra would be tricky.

The three equations are related to the roots of a cubic polynomial.

If the general equation of the polynomial is ax^3+bx^2+cx+d, then we know

The sum of the roots

\alpha+\beta+\gamma=\frac{-b}{a}

The product of the roots

\alpha\beta\gamma=\frac{-d}{a}

and

\alpha\beta+\alpha\gamma+\beta\gamma=\frac{c}{a}

So from our three equations we have

(1)   \begin{equation*}X+Y+Z=10=\frac{-b}{a}\end{equation*}

(2)   \begin{equation*}XYZ=30=\frac{-d}{a}\end{equation*}

(3)   \begin{equation*}XY+YZ+XZ=31=\frac{c}{a}\end{equation*}

Let a=1, then b=-10, c=31, and d=-30

Our cubic is t^3-10t^2+31t-30 and we can try to solve it.

The roots will be factors of -30, so \pm 1, \pm 2, \pm 3, \pm 5, \pm 6, \pm 10, \pm 15, \pm 30

Try t=2

    \begin{equation*}(2)^3-10(2)^2+31(2)-30=0\end{equation}

Hence t=2 is a root.

Use synthetic division to find the quadratic factor

21-1031-30
2-1630
1-8150

The quadratic factor is x^2-8x+15, which factorises to (x-3)(x-5)

Hence the solutions are X=2, Y=3, and Z=5

We could assume the solutions are natural numbers, then we can look at factors of 30.

Factors of ThirtyX+Y+ZXY+YZ+XZ
1, 1, 301+1+30=321+30+30=61
1, 2, 151+2+15=182+15+30=47
1, 5, 61+5+6=125+6+30=41
2, 3, 52+3+5=106+10+15=31

Hence the solutions are X=2, Y=3, and Z=5

But with this approach we might not be able to find the solutions.

Leave a Comment

Filed under Algebra, Cubics, Factorising, Polynomials, Quadratic, Simultaneous Equations, Solving, Sum and Product of Roots

Tagged as , ,

September 19, 2024 · 9:43 am

Solving Cubic Functions

I have been thinking about cubics a bit lately because some of my students are solving and then sketching cubics. Plus I am reading An Imaginary Tale by Paul Nahin, which talks about solving cubics and complex numbers.

Cubics must have at least one real root. If one of the roots is a rational number, then we can use the Factor and Remainder Theorem.

For example,

Solve 2x^3-3x^2-3x+2=0

We know the root(s) must be a factor of 2\times3=6.
I always start with 1 or -1
2(1)^3-3(1)^2-3(1)+2=2-3-3+2=-2 \therefore x\neq=1
Try -1
2(-1)^3-3(-1)^2-3(-1)+2=-2-3+3+2=0 \therefore x=-1 and (x+1) is a factor.
Then we can do polynomial long division.

Now we know that 2x^3-3x^2-3x+2=(x+1)(2x^2-5x+2)
And we can factorise the quadratic (or using the quadratic equation formula)
2x^2-5x+2=2x^2-4x-x+2
=2x(x-2)-1(x-2)
=(2x-1)(x-2)
\therefore x=-1, \frac{1}{2}, 2

But what if it is not factorisable?

For example,

Solve 2x^3+5x^2-2x+4=0

How many roots does this equation have?

We could find the derivative and find out how many stationary points the function has.

f'(x)=6x^2+10x-2

This is a quadratic function. Find the discriminant to determine the number of roots.

\Delta=b^2-4ac=100-4(6)(-2)=148

As \Delta>0, there are two stationary points, which means we could have 1, 2 (one root is repeated) or three roots, depending on if the function crosses the x-axis between stationary points. So not much use.

We could try the discriminant of a cubic.

\Delta=18abcd-4b^3d+b^2c^2-4ac^2-27a^2d^2

\Delta=18(2)(5)(-2)(4)-4(5^3)(4)+(5^2)(-2)^2-4(2)(-2)^2-27(2)^2(4)^2=-5100

The discriminant is negative so there is one real root.

From my reading, we need to turn the cubic into a depressed cubic (cubics of the form x^3+px+q=0).

We can do this by using a change of variable.

Let x=t-\frac{5}{6}
2(x^3+\frac{5}{2}x^2-x+2)=0
\therefore x^3+\frac{5}{2}x^2-x+2=0
Substitute t-\frac{5}{6} into the cubic.
(t-\frac{5}{6})^3+\frac{5}{2}(t-\frac{5}{6})^2-(t-\frac{5}{6})+2
(t^3-3(\frac{5}{6})t^2+3(\frac{5}{6})^2t-(\frac{5}{6})^3+\frac{5}{2}(t^2-2(\frac{5}{6})t+(\frac{5}{6})^2)-t+\frac{5}{6}+2
t^3-\frac{5}{2}t^2+\frac{25}{12}t-\frac{125}{216}+\frac{5}{2}t^2-\frac{25}{6}t+\frac{125}{72}-t+\frac{5}{6}+2
t^3-\frac{37}{12}t+\frac{431}{108}

We can then use Cardano’s formula

x=\sqrt[3]{-\frac{q}{2}+\sqrt{(-\frac{q}{2})^2+(\frac{p}{3})^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{(-\frac{q}{2})^2+(\frac{p}{3})^3}}

p=-\frac{37}{12} and q=\frac{431}{108}
\frac{p}{3}=\frac{-37}{36}
\frac{q}{2}=\frac{431}{216}
(\frac{431}{216})^2+(\frac{-37}{36})^3=\frac{139}{48}
t=\sqrt[3]{\frac{-431}{216}+\sqrt{\frac{139}{48}}}+\sqrt[3]{\frac{-431}{216}-\sqrt{\frac{139}{48}}}
t=-2.21095...
\therefore x=-2.21095...-\frac{5}{6}=-3.044

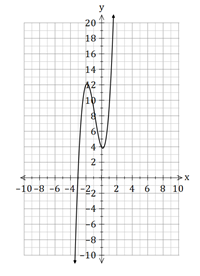
We can see from the sketch below that there is only one solution and it is about -3.

1 Comment

Filed under Cubics, Factorising, Polynomials, Solving

Tagged as , , , , ,