Category Archives: Polynomials

November 22, 2025 · 6:10 am

Polynomial Long Division

I usually choose to use synthetic division when factorising polynomials, but I know some teachers are unhappy when their students do this. So for completeness, here is my PDF for Polynomial Long Division.

Polynomial Long Division Download

Leave a Comment

Filed under Algebra, Cubics, Factorisation, Factorising, Factorising, Polynomials, Quadratics, Solving, Solving, Solving Equations, Year 11 Mathematical Methods

Tagged as polynomial long division, solving cubic equations

October 15, 2025 · 6:19 am

Hard Equation Solving Question

Find the value(s) of $k$ such that the equation below has two numerically equal but opposite sign solutions (e.g. $5$ and $-5$ ).

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{k-1}{k+1}\end{equation}$

$\begin{equation*}(x^2-2x)(k+1)=(k-1)(4x-1)\end{equation}$

$\begin{equation*}(k+1)x^2-2kx-2x=4kx-k-4x+1\end{equation}$

$\begin{equation*}(k+1)x^2-2kx-4kx-2x+4x-1=0\end{equation}$

$\begin{equation*}(k+1)^2x^2-(6k-2)x-1=0\end{equation}$

For there to be two numerically equal but opposite sign solutions, the $b$ term of the quadratic equation must be $0$ .

$\begin{equation*}6k-2=0\end{equation}$

Hence $k=\frac{1}{3}$ .

When $k=\frac{1}{3}$ the equation becomes

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{\frac{-2}{3}}{\frac{4}{3}}\end{equation}$

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{-1}{2}\end{equation}$

$\begin{equation*}2x^2-4x=-4x+1\end{equation}$

$\begin{equation*}2x^2-1=0\end{equation}$

$\begin{equation*}x^2=\frac{1}{2}\end{equation}$

$\begin{equation*}x=\pm \frac{1}{\sqrt{2}}\end{equation}$

Leave a Comment

Filed under Algebra, Polynomials, Quadratic, Quadratics, Solving, Solving, Solving Equations

Tagged as hard algebra question, quadratic, solving quadratic equations

July 11, 2025 · 5:35 am

Simultaneous Equation (or is it?)

Solve simultaneously

$X+Y+Z=10$
$XYZ=30$
$XY+YZ+XZ=31$

We could attempt to solve this simultaneously, but I think the algebra would be tricky.

The three equations are related to the roots of a cubic polynomial.

If the general equation of the polynomial is $ax^3+bx^2+cx+d$ , then we know

The sum of the roots

The product of the roots

and

\alpha\beta+\alpha\gamma+\beta\gamma=\frac{c}{a}

So from our three equations we have

(1) $\begin{equation*}X+Y+Z=10=\frac{-b}{a}\end{equation*}$

(2) $\begin{equation*}XYZ=30=\frac{-d}{a}\end{equation*}$

(3) $\begin{equation*}XY+YZ+XZ=31=\frac{c}{a}\end{equation*}$

Let $a=1$ , then $b=-10, c=31$ , and $d=-30$

Our cubic is $t^3-10t^2+31t-30$ and we can try to solve it.

The roots will be factors of $-30$ , so $\pm 1, \pm 2, \pm 3, \pm 5, \pm 6, \pm 10, \pm 15, \pm 30$

Try $t=2$

$\begin{equation*}(2)^3-10(2)^2+31(2)-30=0\end{equation}$

Hence $t=2$ is a root.

Use synthetic division to find the quadratic factor

$2$	$1$	$-10$	$31$	$-30$
		$2$	$-16$	$30$
	$1$	$-8$	$15$	$0$

The quadratic factor is $x^2-8x+15$ , which factorises to $(x-3)(x-5)$

Hence the solutions are $X=2, Y=3$ , and $Z=5$

We could assume the solutions are natural numbers, then we can look at factors of 30.

Hence the solutions are $X=2, Y=3,$ and $Z=5$

But with this approach we might not be able to find the solutions.

Leave a Comment

Filed under Algebra, Cubics, Factorising, Polynomials, Quadratic, Simultaneous Equations, Solving, Sum and Product of Roots

Tagged as simultaneous equations, solving cubic equations, sum and product of roots

July 1, 2025 · 10:35 am

Synthetic Division (for factorising and/or solving polynomials)

I use synthetic division to factorise polynomials with a degree greater than 2. For example, $f(x)=x^3+2x^2-5x-6$

It works best with monic polynomials but can be adapted to non-monic ones (see example below).

The only problem is that you need to find a root to start.

Try the factors of $-6$ i.e. $(-1, 1, 2, -2, 3, -3, 6, -6)$

$f(-1)=(-1)^3+2(-1)^2-5(-1)-6=0$

Hence, $x=-1$ is a root and $(x+1)$ is a factor of the polynomial.

Set up as follows

Bring the first number down

Multiply by the root and place under the second co-efficient

Add down

Repeat the process

The numbers at the bottom $(1, 1, -6)$ are the coefficients of the polynomial factor.

We now know $x^3+2x^2-5x-6=(x+1)(x^2+x-6)$ .

We can factorise the quadratic in the usual way.

$x^2+x-6=(x+3)(x-2)$

Hence $x^3+2x^2-5x-6=(x+1)(x+3)(x-2)$ .

Let’s try a non-monic example

Factorise $6x^4+39x^3+91x^2+89x+30$

I know $-2$ is a root. Otherwise I would try the factors of 30.

Use synthetic division

Because this was non-monic we need to divide our new co-efficients $(6, 27, 37, 15)$ by 6 (the co-efficient of the $x^4$ term)

$x^3+\frac{9}{2}x^2+\frac{37}{6}+\frac{5}{2}$

We now need to go again. I know that $\frac{-3}{2}$ is a root and $(2x+3)$ is a factor.

Our quadratic factor is $x^2+3x+5/3$ , which is $3x^2+9x+5$ .

The quadratic factor doesn’t have integer factors so,

$6x^4+39x^3+91x^2+89x+30=(x+2)(2x+3)(3x^2+9x+5)$

I think this is much quicker than polynomial long division.

1 Comment

Filed under Algebra, Factorising, Factorising, Fractions, Polynomials, Quadratic, Simplifying fractions, Solving Equations

Tagged as non monic synthetic division, Synthetic division

April 30, 2025 · 6:08 am

Factorising Non-Monic Quadratics

The general equation of a quadratic is $ax^2+bx+c$

Let’s explore different methods of factorising a non-monic quadratic (the $a$ term is not $1$ )

Factorise $6x^2+x-12$

We need to find two numbers that add to $1$ and multiply to $-72$ (i.e. add to $b$ and multiply to $a\times c)$

The two numbers are $9$ and $-8$

Method 1 – Splitting the middle term

This is the method I teach the most often

$\begin{equation*}6x^2+x-12\end{equation}$

Split the middle term (the $b$ term) into the two numbers

$\begin{equation*}6x^2-8x+9x-12\end{equation}$

The order doesn’t matter.

Find a common factor for the first term terms, and then for the last two terms.

$\begin{equation*}2x(3x-4)+3(3x-4)\end{equation}$

There is a common factor of $(3x-4)$ , factor it out.

$\begin{equation*}(3x-4)(2x+3)\end{equation}$

Method two – Fraction

$\begin{equation*}6x^2+x-12\end{equation}$

Put $6x$ into both factors and divide by $6$

$\begin{equation*}\frac{(6x-8)(6x+9)}{6}\end{equation}$

Factorise

$\begin{equation*}\frac{2(3x-4)3(2x+3)}{6}\end{equation}$

$\begin{equation*}\frac{6(3x-4)(2x+3)}{6}\end{equation}$

$\begin{equation*}(3x-4)(2x+3)\end{equation}$

Method 3 – Monic to non-monic

$\begin{equation*}y=6x^2+x-12\end{equation}$

Multiply both sides of the equation by $a$

$\begin{equation*}6y=6(6x^2+x-12)\end{equation}$

$\begin{equation*}6y=6^2x^2+6x-72\end{equation}$

$\begin{equation*}6y=(6x)^2+6x-72\end{equation}$

Let $A=6x$

$\begin{equation*}6y=A^2+A-72\end{equation}$

Factorise

$\begin{equation*}6y=(A+9)(A-8)\end{equation}$

Replace the $A$ with $6x$

$\begin{equation*}6y=(6x+9)(6x-8)\end{equation}$

$\begin{equation*}6y=3(2x+3)2(3x-4)\end{equation}$

$\begin{equation*}6y=6(2x+3)(3x-4)\end{equation}$

$\begin{equation*}y=(2x+3)(3x-4)\end{equation}$

Method 4 – Cross Method

$\begin{equation*}6x^2+x-12\end{equation}$

Place the two numbers in the cross

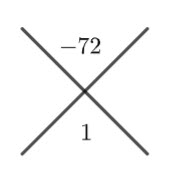
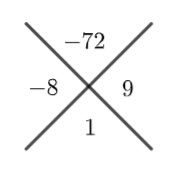
Place the two numbers that add to $1$ and multiply to $-72$ in the other parts of the cross.

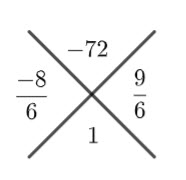
Divide these two numbers by $6$ (i.e $a$ )

Simplify

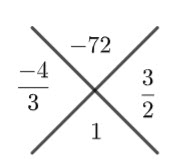
Hence,

$\begin{equation*}(x-\frac{4}{3})(x+\frac{3}{2})\end{equation}$

Which is

$\begin{equation*}(3x-4)(2x+3)\end{equation}$

Method 5 – By Inspection

This is my least favourite method – although students get better with practice

$\begin{equation*}6x^2+x-12\end{equation}$

The factors of $a$ are $1, 2, 3,$ and $6$ and the factors of $12$ are $1, 2, 3, 4, 6, 12$

We know one number is positive and one number negative.

Which give us all of these possibilities

$\begin{equation*}(2x+3)(3x-4)\end{equation}$

With a bit of practice you don’t need to check all of the possibilties, but I find students struggle with this method.

Method 6 – Grid

$\begin{equation*}6x^2+x-12\end{equation}$

Create a grid like the one below


	$6x^2$
		$-12$

Find the two numbers that multiply to $-72$ and add to $1$ and place them in the other grid spots (see below)


	$6x^2$	$-8x$
	$9x$	$-12$

Find the HCF (highest common factor) of each row and put in the first column.

Row $1$ HCF= $2x$ , Row $2$ HCF= $3$


$2x$	$6x^2$	$-8x$
$3$	$9x$	$-12$

For the columns, calculate what is required to multiple the HCF to get the table entry.

For example, what do you need to multiple $2x$ and $3$ by to get $6x^2$ and $9x$ ? In this case it is $3x$ . It’s always going to be the same thing, so just use one value to calculate it,

	$3x$	$-4$
$2x$	$6x^2$	$-8x$
$3$	$9x$	$-12$

The factors are column $1$ and row $1$
$(2x+3)(3x-4)$

The two methods I use the most are splitting the middle term, and the cross method, but I can see value in the grid method.

Leave a Comment

Filed under Algebra, Factorising, Factorising, Polynomials, Quadratic, Quadratics

Tagged as Factorising, factorising non-monic trinomials, non-monic quadratics

March 31, 2025 · 7:14 am

Deriving the Quadratic Equation formula

My year 10 students have been learning how to complete the square with the idea of then deriving the quadratic equation formula.

The general equation for a quadratic is $y=ax^2+bx+c$

Completing the square,

$\begin{equation*}ax^2+bx+c\end{equation}$

Factorise out the leading coefficient (i.e. $a$ )

$\begin{equation*}a(x^2+\frac{bx}{a}+\frac{c}{a})\end{equation}$

Half the second term (i.e $\frac{b}{a}$ ) and subtract the square of the second term.

$\begin{equation*}a((x+\frac{b}{2a})^2-(\frac{b}{2a})^2+\frac{c}{a})\end{equation}$

$\begin{equation*}a((x+\frac{b}{2a})^2-\frac{b^2}{4a^2}+\frac{c}{a})\end{equation}$

Simplify

$\begin{equation*}a((x+\frac{b}{2a})^2-\frac{b^2}{4a^2}+\frac{4ac}{4a^2})\end{equation}$

$\begin{equation*}a((x+\frac{b}{2a})^2+\frac{-b^2+4ac}{4a^2})\end{equation}$

$\begin{equation*}a(x+\frac{b}{2a})^2+\frac{-b^2+4ac}{4a}\end{equation}$

Now let’s solve

$\begin{equation*}a(x+\frac{b}{2a})^2+\frac{-b^2+4ac}{4a}=0\end{equation}$

$\begin{equation*}a(x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a}\end{equation}$

$\begin{equation*}(x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a^2}\end{equation}$

$\begin{equation*}(x+\frac{b}{2a})=\pm \sqrt{\frac{b^2-4ac}{4a^2}}\end{equation}$

$\begin{equation*}(x+\frac{b}{2a})=\frac{\pm \sqrt{b^2-4ac}}{2a}\end{equation}$

$\begin{equation*}x=-\frac{b}{2a}\frac{\pm \sqrt{b^2-4ac}}{2a}\end{equation}$

Which is the quadratic equation formula.

1 Comment

Filed under Algebra, Quadratic, Quadratics, Solving, Solving, Solving Equations

Tagged as completing the square, quadratic equation formula

November 26, 2024 · 7:07 am

Infinite Product Expansion of cos (x)

Remember

(1) $\begin{equation*}cos(x)=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+...\end{equation*}$

We know that $cos(x)=0$ for odd integer multiples of $\frac{\pi}{2}$ , i.e. $\frac{\pi}{2}, \frac{3\pi}{2}, ...$ , which is $\frac{(2n-1)\pi}{2}$ for $n\neq 0$

Hence,

$\begin{equation*}0=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+...\end{equation}$

for $x=\frac{(2n-1)\pi}{2}, n>0$

We can factorise our $cos(x)$ expansion

$\begin{equation*}(1-\frac{x^2}{r_1})(1-\frac{x^2}{r_2})...\end{equation}$

We know $r_1=\frac{\pi}{2}, r_2=\frac{3\pi}{2}, ...$

$\begin{equation*}cos(x)=(1-\frac{x^2}{(\frac{\pi}{2})^2})(1-\frac{x^2}{(\frac{3\pi}{2})^2})...(1-\frac{x^2}{(\frac{(2n-1)\pi}{2})^2})\end{equation}$

$\begin{equation*}cos(x)=\Pi_{n=1}^{\infty}(1-\frac{x^2}{(\frac{(2n-1)\pi}{2})^2})\end{equation}$

$\begin{equation*}cos(x)=\Pi_{n=1}^{\infty}(1-\frac{4x^2}{(2n-1)^2\pi^2})\end{equation}$

1 Comment

Filed under Factorising, Identities, Infinite Product Expansion, Interesting Mathematics, Polynomials, Trigonometry

Tagged as infinite product expansion of cos(x), trigonometry

September 19, 2024 · 9:43 am

Solving Cubic Functions

I have been thinking about cubics a bit lately because some of my students are solving and then sketching cubics. Plus I am reading An Imaginary Tale by Paul Nahin, which talks about solving cubics and complex numbers.

Cubics must have at least one real root. If one of the roots is a rational number, then we can use the Factor and Remainder Theorem.

For example,

Solve $2x^3-3x^2-3x+2=0$

But what if it is not factorisable?

For example,

Solve $2x^3+5x^2-2x+4=0$

How many roots does this equation have?

We could find the derivative and find out how many stationary points the function has.

$f'(x)=6x^2+10x-2$

This is a quadratic function. Find the discriminant to determine the number of roots.

$\Delta=b^2-4ac=100-4(6)(-2)=148$

As $\Delta>0$ , there are two stationary points, which means we could have 1, 2 (one root is repeated) or three roots, depending on if the function crosses the $x-$ axis between stationary points. So not much use.

We could try the discriminant of a cubic.

$\Delta=18abcd-4b^3d+b^2c^2-4ac^2-27a^2d^2$

$\Delta=18(2)(5)(-2)(4)-4(5^3)(4)+(5^2)(-2)^2-4(2)(-2)^2-27(2)^2(4)^2=-5100$

The discriminant is negative so there is one real root.

From my reading, we need to turn the cubic into a depressed cubic (cubics of the form $x^3+px+q=0$ ).

We can do this by using a change of variable.

We can then use Cardano’s formula

$x=\sqrt[3]{-\frac{q}{2}+\sqrt{(-\frac{q}{2})^2+(\frac{p}{3})^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{(-\frac{q}{2})^2+(\frac{p}{3})^3}}$

$p=-\frac{37}{12}$ and $q=\frac{431}{108}$
$\frac{p}{3}=\frac{-37}{36}$
$\frac{q}{2}=\frac{431}{216}$
$(\frac{431}{216})^2+(\frac{-37}{36})^3=\frac{139}{48}$
$t=\sqrt[3]{\frac{-431}{216}+\sqrt{\frac{139}{48}}}+\sqrt[3]{\frac{-431}{216}-\sqrt{\frac{139}{48}}}$
$t=-2.21095...$
$\therefore x=-2.21095...-\frac{5}{6}=-3.044$

We can see from the sketch below that there is only one solution and it is about $-3$ .

1 Comment

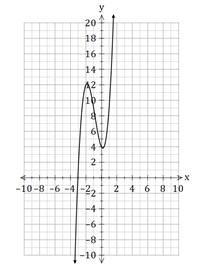
Filed under Cubics, Factorising, Polynomials, Solving

Tagged as Cardano, Cubics, Depressed Cubic, Factorising, Polynomials, Solving

September 14, 2024 · 9:45 am

Sum and Product of the Roots of Polynomials

There is a relationship between the sum and product of the roots of a polynomial and the co-efficient of the polynomial.

Let’s start with a quadratic.

The general form for a quadratic (polynomial of degree 2) is

$y=ax^2+bx+c$

Use the quadratic equation formula to find the roots

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

Hence the roots are

$x_1=\frac{-b+\sqrt{b^2-4ac}}{2a}$ and $x_2=\frac{-b-\sqrt{b^2-4ac}}{2a}$

Sum of the roots:

$\frac{-b+\sqrt{b^2-4ac}}{2a}+\frac{-b-\sqrt{b^2-4ac}}{2a}=\frac{-2b}{2a}=\frac{-b}{a}$

Product of the roots:

$\frac{-b+\sqrt{b^2-4ac}}{2a}\times\frac{-b-\sqrt{b^2-4ac}}{2a}$

$\frac{b^2}{4a^2}-\frac{b^2-4ac}{4a^2}$

$\frac{4ac}{4a^2}$

$\frac{a}{c}$

Let’s move to a cubic function.

The general equation is $f(x)=ax^3+bx^2+cx+d$

Let’s say the roots of this cubic are $\alpha, \beta, \gamma$

Then $ax^3+bx^2+cx+d=a(x-\alpha)(x-\beta)(x-\gamma)$

$=a(x^2-\beta x - \alpha x+\alpha\beta)(x-\gamma)$

$=a(x^2-(\alpha+\beta)x+\alpha\beta)(x-\gamma)$

$=a(x^3-\gamma x^2-x^2(\alpha+\beta)+\gamma(\alpha+\beta)x-\alpha\beta\gamma)$

$=a(x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\alpha\gamma+\beta\gamma)x-\alpha\beta\gamma)$

The sum of the roots

$\alpha+\beta+\gamma=\frac{-b}{a}$

The product of the roots

$\alpha\beta\gamma=\frac{-d}{a}$

Also, it can be handy to know

$\alpha\beta+\alpha\gamma+\beta\gamma=\frac{c}{a}$

We can extend the method we used for finding the sum and product of the roots of cubic to polynomials of greater degree.

If the four roots of a quartic are $\alpha, \beta, \gamma$ and $\delta$ , and the general equation is $ax^4+bx^3+cx^2+dx+e$ , then

$\alpha+\beta+\gamma+\delta=\frac{-b}{a}$

$\alpha\beta+\alpha\gamma+\alpha\delta+\beta\gamma+\beta\delta+\gamma\delta=\frac{c}{a}$

$\alpha\beta\gamma+\alpha\beta\delta+\alpha\gamma\delta+\beta\gamma\delta=\frac{-d}{a}$

$\alpha\beta\gamma\delta=\frac{e}{a}$

1 Comment

Filed under Polynomials, Sum and Product of Roots

Tagged as Polynomials, product, sum, sum and product of polynomials

July 16, 2024 · 7:35 am

Australian Mathematics Competition – Polynomial Question

I came across this question from the 2010 Senior Australian Mathematics Competition:

A polynomial $f$ is given. All we know about it is that all its coefficients are non-negative integers, $f(1)=6$ and $f(7)=3438$ . What is the value of $f(3)$
Australian Mathematics Competition 2006-2012

I thought ‘excellent, a somewhat hard polynomial question for my students’ and then I tried it. Now I know why only 1% of students got it correct.

As we don’t know the order of the polynomial, let

$f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x^1+a_0$

We know all of the coefficients are greater than or equal to zero. We also know

$f(1)=a_n+a_{n-1}+...+a+a_0=6$

Which means that all of the coefficients are between zero and six

$0\le{a_n}\le{6}$

We have also been given $f(7)$

$f(7)=7^na_n+7^{n-1}a_{n-1}+ ... +7a+1=3438$

As all of the coefficients are between zero and six, this is $3438$ written in base 7.

Let’s calculate a few powers of 7

	Powers of 7
$7^0$	1
$7^1$	7
$7^2$	49
$7^3$	343
$7^4$	2401
$7^5$	16807

Hence $3438$ written in base $7$ is $13011$

Therefore $f(x)=x^4+3x^3+x+1$

$f(3)=3^4+3\times3^3+3+1$

$f(3)=81+81+4$

$f(3)=166$

I really like this question. I think it could work well as a class extension activity with a bit of scaffolding.

Leave a Comment

Filed under Number Bases, Polynomials

Tagged as base 7, number bases, Polynomials

Factors of Thirty	$X+Y+Z$	$XY+YZ+XZ$
$1, 1, 30$	$1+1+30=32$	$1+30+30=61$
$1, 2, 15$	$1+2+15=18$	$2+15+30=47$
$1, 5, 6$	$1+5+6=12$	$5+6+30=41$
$2, 3, 5$	$2+3+5=10$	$6+10+15=31$

Possible factorisations	$b$ term of expansion
$(x-1)(6x+12)$	$12x-6x=6x$	No
$(x-2)(6x+6)$	$6x-12x=-6x$	No
$(x-3)(6x+4)$	$4x-18x-14x$	No
$(2x-1)(3x+12)$	$24x-3x=21x$	No
$(2x-2)(3x+6)$	$12x-6x=6x$	No
$(2x-3)(3x+4)$	$8x-9x=-1x$	Almost, switch the signs
$(2x+3)((3x-4)$	$-8x+9x=1x$	Yes

As numbers	As Powers of 7
$3438=1\times2401+1037$	$3438=1\times7^4+1037$
$1037=3\times343+8$	$1037=3\times7^3+8$
$8=1\times7+1$	$8=1\times7^1+1$
$1=1\times1$	$1=1\times7^0$

Category Archives: Polynomials

Polynomial Long Division

Hard Equation Solving Question

Simultaneous Equation (or is it?)

Synthetic Division (for factorising and/or solving polynomials)

Factorising Non-Monic Quadratics

Method 1 – Splitting the middle term

Method two – Fraction

Method 3 – Monic to non-monic

Method 4 – Cross Method

Method 5 – By Inspection

Method 6 – Grid

Deriving the Quadratic Equation formula

Infinite Product Expansion of cos (x)

Solving Cubic Functions

Sum and Product of the Roots of Polynomials

Australian Mathematics Competition – Polynomial Question

Recent Posts

Categories

Archives