I think this one is doing the rounds, I first saw it here.
![]()
![]() is the obvious answer,
is the obvious answer, ![]() , but are there more answers?
, but are there more answers?
This was my approach
![]()
![]()
![]()
![]()
A quadratic equation.
Hence,
![]()
I then used my calculator
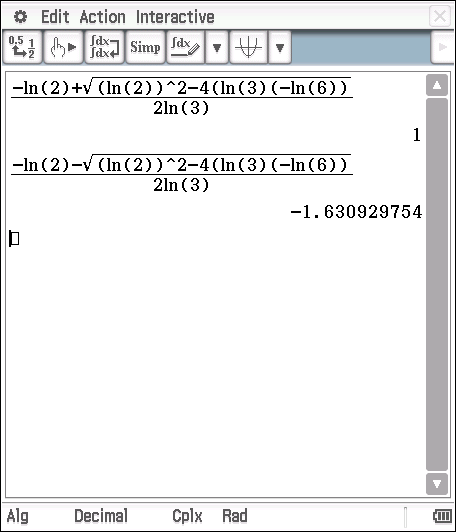
Hence ![]() 0r
0r ![]()
I think this one is doing the rounds, I first saw it here.
![]()
![]() is the obvious answer,
is the obvious answer, ![]() , but are there more answers?
, but are there more answers?
This was my approach
![]()
![]()
![]()
![]()
A quadratic equation.
Hence,
![]()
I then used my calculator

Hence ![]() 0r
0r ![]()
Filed under Algebra, Index Laws, Interesting Mathematics, Quadratics, Solving
Remember
(1) ![]()
We know that ![]() for odd integer multiples of
for odd integer multiples of ![]() , i.e.
, i.e. ![]() , which is
, which is ![]() for
for ![]()
Hence,
![]()
for ![]()
We can factorise our ![]() expansion
expansion
![]()
We know ![]()
![]()
![]()
![]()
I have been reading An Imaginary Tale – The Story of ![]() by Paul J Nahin, which is fabulous. There was a bit in chapter 4 where he found the closed form of the generalised Fibonacci sequence. I thought it would be a good exercise to find the closed from of the Fibonacci sequence.
by Paul J Nahin, which is fabulous. There was a bit in chapter 4 where he found the closed form of the generalised Fibonacci sequence. I thought it would be a good exercise to find the closed from of the Fibonacci sequence.
Just to remind you, the Fibonacci sequence is
![]()
and it is defined recursively
![]()
That is, the next term is the sum of the two previous terms, i.e.
![]()
Now the starting off point is slightly dodgy as it involves and educated guess as Paul Nahin writes,
How do I know that works? Because I have seen it before, that’s how! […] There is nothing dishonourable about guessing correct solutions – indeed, great mathematicians and scientists, are invariable great guessers – just as long as eventually the guess is verified to work. The next time you encounter a recurrence formula, you can guess the answer too because then you will have already seen how it works.
We start with ![]()
This means ![]() is
is ![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
Hence ![]() and we can use the initial conditions
and we can use the initial conditions ![]() and
and ![]() to find
to find ![]() and
and ![]()
When ![]()
(1) ![]()
When ![]()
(2) ![]()
From equation ![]() ,
, ![]() , substitute into equation
, substitute into equation ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Does it work?
Remember the sequence is ![]()
If ![]()
![]()

As you can see it works!
This is one of those theorems, where the name is probably not the person who discovered it. Check out the Wikipedia entry for more information on the history.
Napoleon’s theorem states that if equilateral triangles are constructed on the sides of any triangle, either all outward or all inward, the lines connecting the centres of those equilateral triangles themselves form an equilateral triangle.
I am just going to look at the outward triangles.
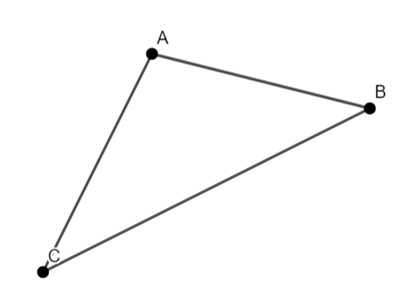
Construct equilateral triangles on the edges AB, BC and AC.
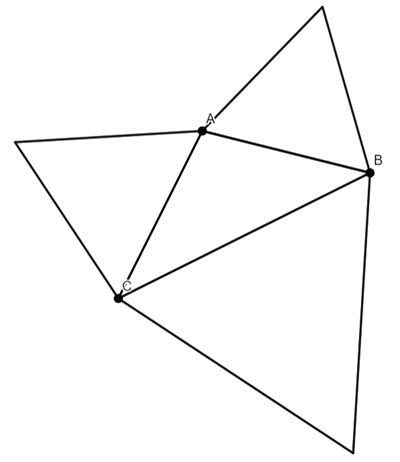
Find the centre (Centroid) of these triangles.
Note: The centroid is the point of intersections of the medians.
A median is the line from a vertex to the midpoint of the opposite side.
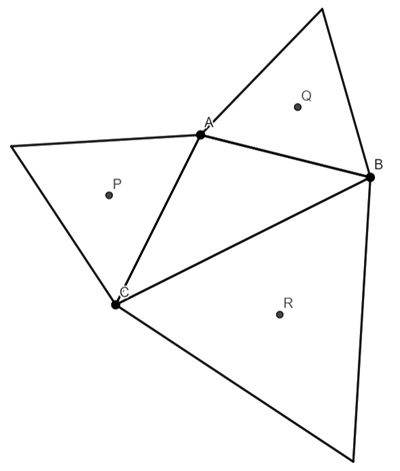
We are going to prove that triangle PQR is equilateral
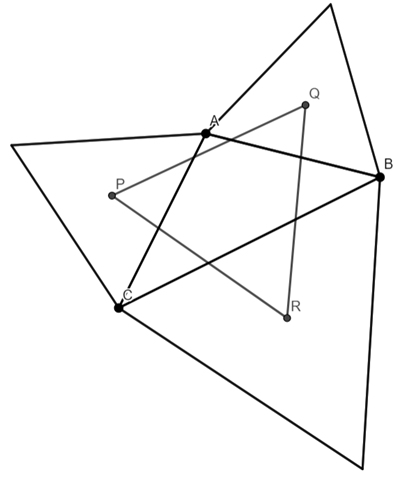
I am going to add AP, AQ, QB, BR, RC and CP
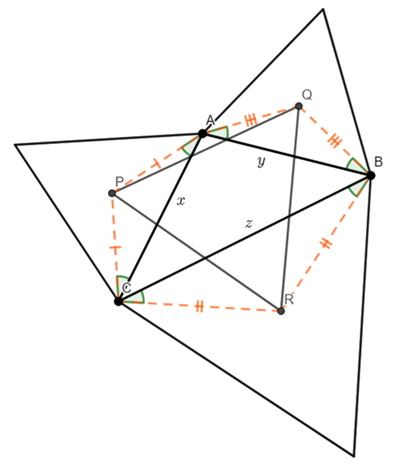
As P, Q and R are the centroids, PA=PC, QA=QB, and RB=RC.
Therefore triangles AQB, BRC, and CPA are isosceles.
The angles QAB, QBA, RBC, RCB, PCA, PAC (the shaded angles in the above diagram) are 30 degrees, because the line bisects the angle (and the angle is 60 degrees because the triangles are equilateral).
Now for the maths.
![]()
![]()
![]()
![]()
PA is 2/3 the length of the median.
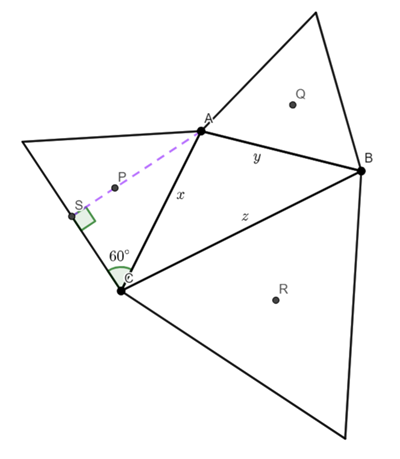
AS is the median
![]()
![]()
![]()
Hence,
![]()
![]()
![]()
In the same manner,
![]()
Using the cosine rule
![]()
![]()
![]()
![]()
![]()
Now from the original triangle ABC
![]()
![]()
![]()
Multiply both sides by 3 and expand and simplify
![]()
![]()
![]()
We are going to do the same for QR
![]()
![]()
![]()
Once again, from triangle ABC
![]()
![]()
![]()
Multiply both sides by three and expand and simplify
![]()
![]()
![]()
We can do the same for PR
![]()
![]()
![]()
And from triangle ABC
![]()
![]()
![]()
Multiply both sides by three and expand and simplify
![]()
Hence, PQ=PR=RQ and triangle PQR is equilateral.
Filed under Interesting Mathematics, Napoleon's Triangle