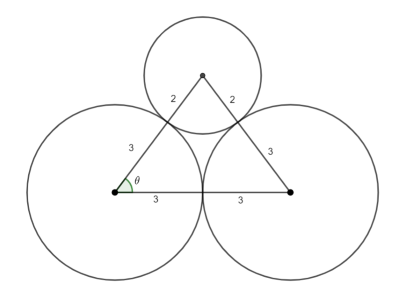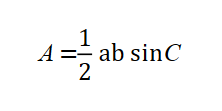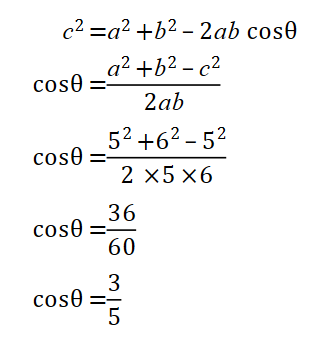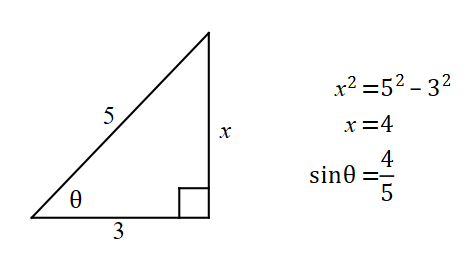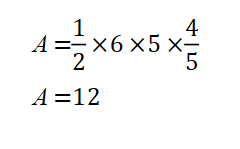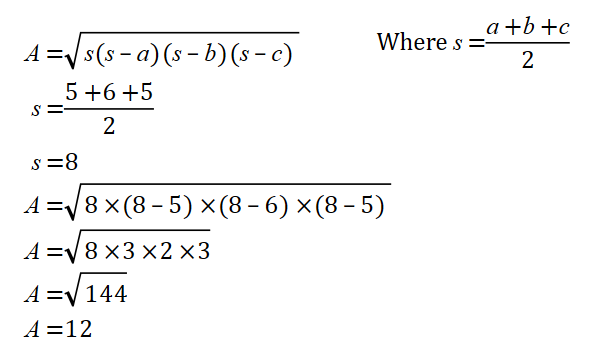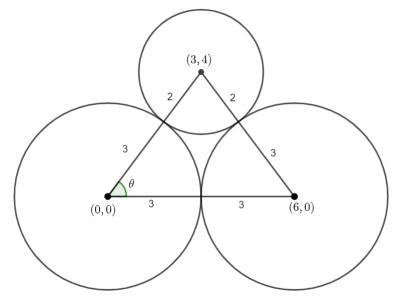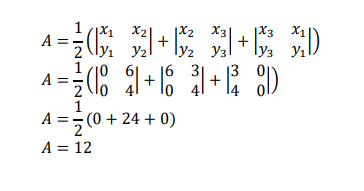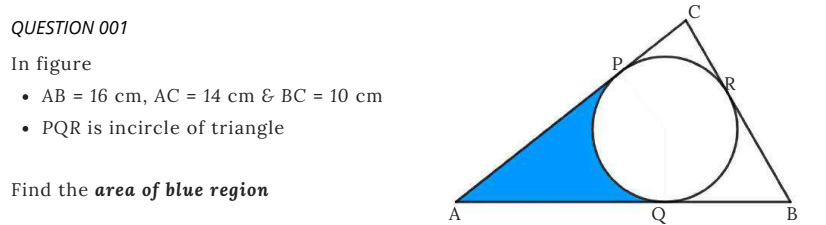
The blue shaded area is the area of triangles ![]() and
and ![]() subtract the sector
subtract the sector ![]() .
.
We can use Heron’s law to find the area of the triangle ![]()
![]()
where ![]()
![]()
We also know the area of triangle ![]() where
where ![]() is the radius of the inscribed circle.
is the radius of the inscribed circle.
Hence, ![]() and
and ![]()
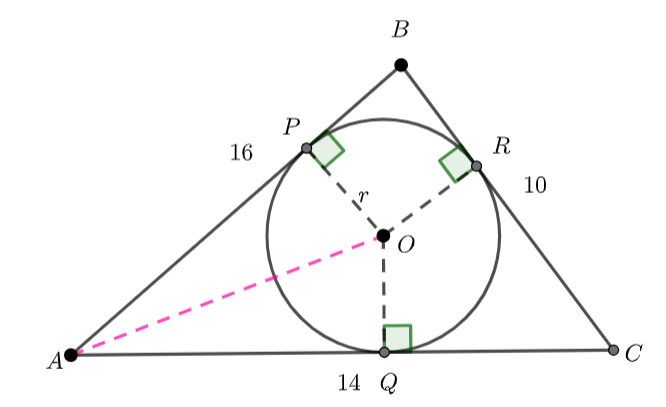
We know ![]() , and
, and ![]() – tangents to a circle are congruent.
– tangents to a circle are congruent.
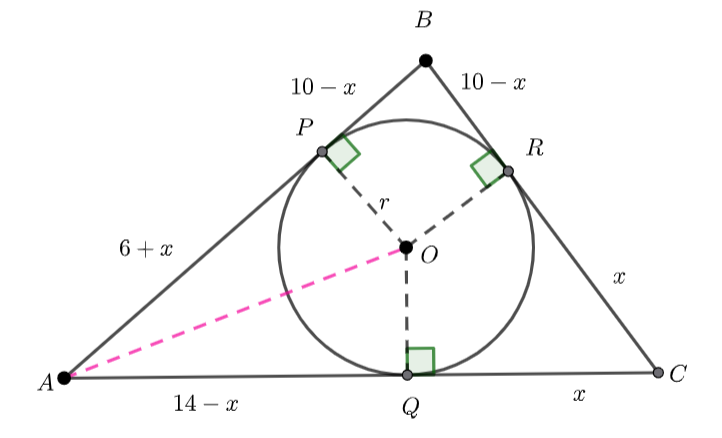
![]()
(1) ![]()
(2) ![]()
Area ![]()
Area ![]() Area
Area ![]()
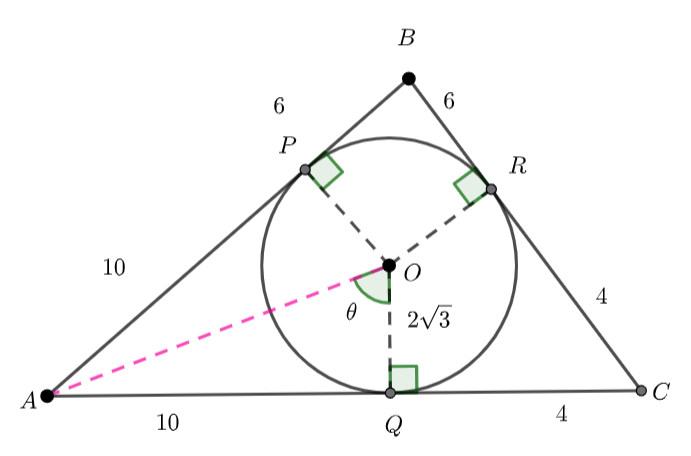
![]()
![]()
Area of sector ![]()
Blue area = ![]()