Solve ![]() for
for ![]()
Remember the identity
(1) ![]()
Hence
![]()
Now I have
![]()
![]()
![]() or
or ![]()
![]()
![]() for
for ![]()
![]()
![]()
Hence ![]()
Solve ![]() for
for ![]()
Remember the identity
(1) ![]()
Hence
![]()
Now I have
![]()
![]()
![]() or
or ![]()
![]()
![]() for
for ![]()
![]()
![]()
Hence ![]()
I usually choose to use synthetic division when factorising polynomials, but I know some teachers are unhappy when their students do this. So for completeness, here is my PDF for Polynomial Long Division.
In the diagram below, ![]() and
and ![]() lie on the circle with centre
lie on the circle with centre ![]() . If
. If ![]() and
and ![]() , determine with reasoning
, determine with reasoning ![]() and
and ![]()

We know ![]() – radii of the circle.
– radii of the circle.
Which means, ![]() is isosceles and
is isosceles and ![]() – equal angles isosceles triangle.
– equal angles isosceles triangle.
![]() – angle at the centre twice the angle at the circumference.
– angle at the centre twice the angle at the circumference.
![]()

This means ![]() – angles on a straight line are supplementary
– angles on a straight line are supplementary
![]() – equal angles isosceles triangle and the angle sum of a triangle.
– equal angles isosceles triangle and the angle sum of a triangle.
![]() – angle at the circumference subtended by the same arc are congruent.
– angle at the circumference subtended by the same arc are congruent.

![]() – angles at the circumference subtended by the same arc are congruent.
– angles at the circumference subtended by the same arc are congruent.
![]() – equal angle isosceles triangle
– equal angle isosceles triangle
Hence ![]()
Completing the square is useful to
When completing the square we take advantage of perfect squares. For example, ![]()
![]() and
and ![]()
Put ![]() into completed square form.
into completed square form.
What perfect square has an ![]() term?
term?
![]()
We don’t want ![]() , we want
, we want ![]() , so subtract
, so subtract ![]()
![]()
![]()
What about a non-monic quadratic? For example,
![]()
Factorise the ![]()
![]()
And continue as before
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A circle has equation
(a) Find the centre and radius of the circle.
Pointsand
lie on the circle such that the origin is the midpoint of
.
(b) Show thathas a length of 12.
(a)We need to put the circle equation into completed square form
![]()
![]()
The centre is ![]() and the radius is
and the radius is ![]() .
.
(b)Draw a diagram
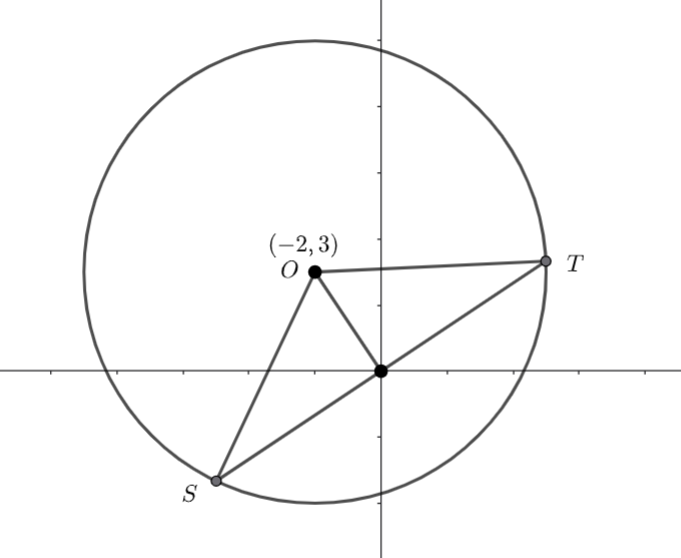
We know ![]() and
and ![]() are radii of the circle. Hence
are radii of the circle. Hence ![]() is isosceles and the line segment from
is isosceles and the line segment from ![]() to the origin is perpendicular to
to the origin is perpendicular to ![]() .
.
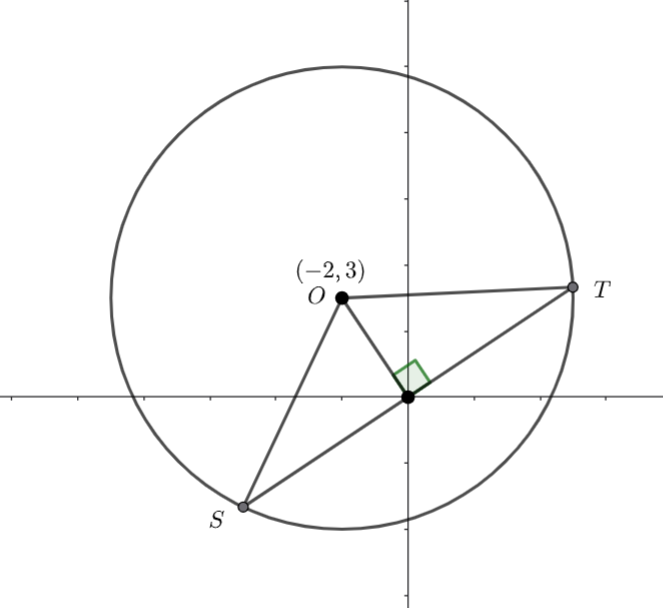
![]() and the distance from
and the distance from ![]() to the origin is
to the origin is
![]()
We can use Pythagoras to find the distance from the origin to ![]() .
.
![]()
Hence ![]()