We are going to derive the transformation matrix for a reflection across a line ![]() .
.

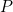 across the line to
across the line to 
Things to remember about a reflection:
- The distance between
 and the line is same as the distance between
and the line is same as the distance between 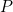 and the line. Hence
and the line. Hence 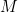 is the midpoint of
is the midpoint of 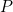 and
and  .
. - The line segment joining
 and
and  is perpendicular to the line.
is perpendicular to the line.
Our aim is to find a general identity for ![]() and then use that to derive a transformation matrix.
and then use that to derive a transformation matrix.
Let’s start by finding the equation of the line joining ![]() and
and ![]() .
.
We know the gradient of this line is perpendicular to the gradient of ![]() , hence the gradient is
, hence the gradient is ![]() .
.
![]()
And ![]() is a point on the line.
is a point on the line.
![]()
Which simplifies to
(1) ![]()
We are going to find the co-ordinates of ![]() in two ways; as the midpoint of
in two ways; as the midpoint of ![]() and
and ![]() , and as the point of intersection of
, and as the point of intersection of ![]() and
and ![]()
As the midpoint of ![]() and
and ![]()
(2) ![]()
As the point of intersection of ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
Substitute ![]() into
into ![]()
![]()
(3) ![]()
![]() must equal
must equal ![]() , hence we can find
, hence we can find ![]() in terms of
in terms of ![]()
Equate equation ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
(4) ![]()
And
![]()
![]()
![]()
![]()
![]()
![]()
(5) ![]()
Hence ![]()
For ease of writing, let ![]() and
and ![]()
Then
![]() , which we can generalise to
, which we can generalise to ![]()
Now let’s think about a transformation matrix, we want to transform ![]() to
to ![]()
![]()
Remember the gradient of a line is the tangent of the angle of inclination, ![]()
![]()
Remember the identity
![]()
![]()
![]()
![]()
![]()
(6) ![]()
And we will do the same for ![]() .
.
![]()
![]()
![]()
![]()
(7) ![]()
Hence our transformation matrix is
(8) ![]()
Example
The vertices of a triangle
are
and
.
is a reflection of
in the line
The gradient of the line
is
.
Our transformation matrix is
Which is
So
