Tag Archives: matrix tranformations

September 9, 2025 · 11:19 am

Linear Transformation (Rotation) Question

The unit square is rotated about the origin by 45^\circ anti-clockwise.
(a) Find the matrix of this transformation.
(b) Draw the unit square and its image on the same set of axes.
(c) Find the area of the over lapping region.

Remember the general rotation matrix is

    \begin{equation*}\begin{bmatrix}cos(\theta)&-sin(\theta)\\sin(\theta)&cos(\theta)\end{bmatrix}\end{equation}

Hence

    \begin{equation*}\begin{bmatrix}cos(45)&-sin(45)\\sin(45)&cos(45)\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}\end{equation}

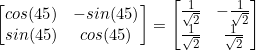
The unit square has co-ordinates

\begin{bmatrix}0 & 1 & 1& 0\\0&0&1&1\end{bmatrix}

Unit Square

Transform the unit square

\begin{bmatrix}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}\begin{bmatrix}0 & 1 & 1& 0\\0&0&1&1\end{bmatrix}=\begin{bmatrix}0&\frac{1}{\sqrt{2}}&0&-\frac{1}{\sqrt{2}}\\0&\frac{1}{\sqrt{2}}&\frac{2}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}

Unit Square and Transformed Unit Square

The overlapping area is the area of \Delta ADC– the area of \Delta EFC

We know \angle{FCE}=45^\circ because the diagonal of a square bisects the angle.

We know\angle{EFC} is a right angle as it’s on a straight line with the vertex of a square.

Hence \Delta EFC is isosceles.

\overline{AC}=\sqrt{1^2+1^2}=\sqrt{2} and \overline{AF}=1, hence \overline{FC}=\sqrt{2}-1

A_{\Delta ADC}=\frac{1}{2}(1)(1)=\frac{1}{2}

A_{\Delta ECF}=\frac{1}{2}(\sqrt{2}-1)(\sqrt{2}-1)

Area of shaded region =\frac{1}{2}-\frac{1}{2}(3-2\sqrt{2})=\sqrt{2}-1

Leave a Comment

Filed under Area, Co-ordinate Geometry, Finding an area, Geometry, Matrices, Transformations, Year 11 Specialist Mathematics

Tagged as ,