Tag Archives: general solution to trig equations

July 26, 2025 · 8:45 am

General Solutions to Trigonometric Equations

Solve $sinx=\frac{1}{2}$ for $0\le x \le 2\pi$

Sine is positive in the first and second quadrants.

$\begin{equation*}sinx=\frac{1}{2}\end{equation}$

$\begin{equation*}x=\frac{\pi}{6} \text{ and } x=\pi-\frac{\pi}{6}=\frac{5\pi}{6}\end{equation}$

But what if we aren’t given a domain for the $x$ values?

Then we need to give general solutions.

For example,

Solve $sinx=\frac{1}{2}$

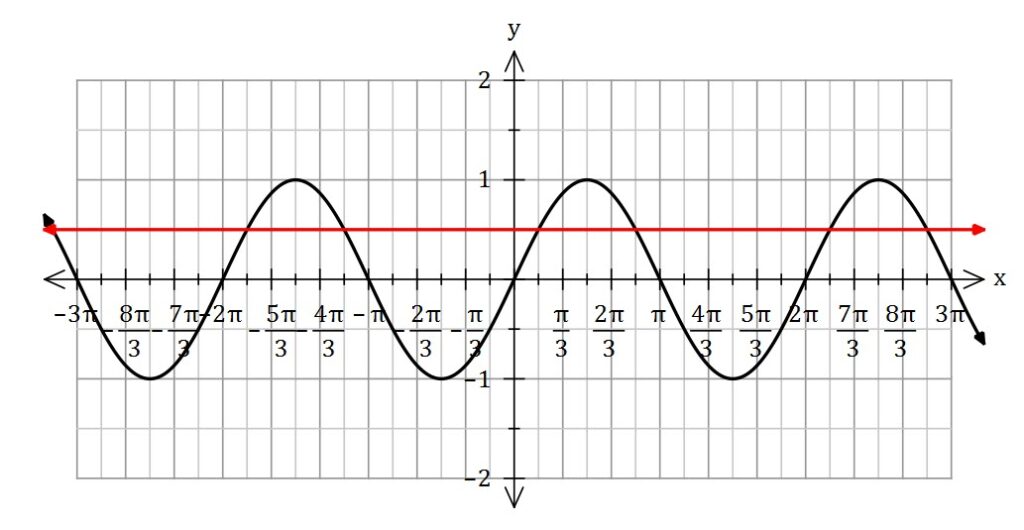
As you can see from the sketch above, there are infinite solutions.

The sine function has a period of $360^\circ$ , and so if $\frac{\pi}{6}$ is a solution then $\2pi+\frac{\pi}{6}$ is also a solution. This means $\frac{\pi}{6}+2\pi n, n\in\mathbb{Z}$ is a general solution. And we can do the same for the second solution $\frac{5\pi}{6}+2\pi n$ .

In general

$\begin{equation*}sinx=y\end{equation}$

$\begin{equation*}x=arcsin(y)+2\pi n \text { and } x=\pi-arcsin(y)+2\pi n \end{equation}$

$\begin{equation*}x=arcsin(y)+2\pi n \text { and } x=\pi(2n+1)-arcsin(y), n \in \mathbb{Z}\end{equation}$

We can turn this into one equation
$\begin{equation*}x=(-1)^n arcsin(y)+n\pi, n \in \mathbb{Z}\end{equation}$

What about cosine?

Solve $cosx=\frac{1}{2}$

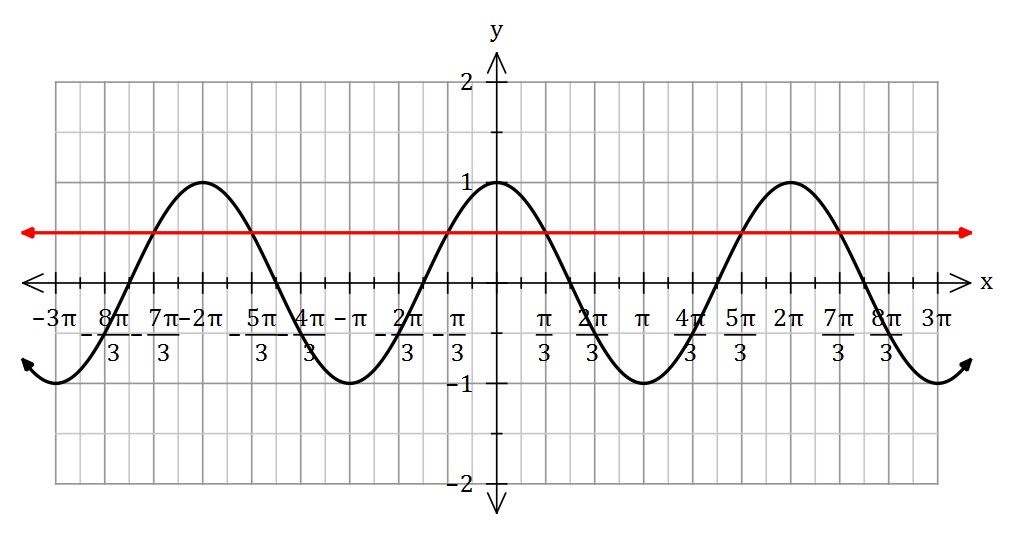
Cosine is positive in the first and fourth quadrants (it also has a period of $2\pi$ . The first two (positive) solutions are $\frac{\pi}{3}$ and $2\pi-\frac{\pi}{3}$ .

To generalise, $x=2\pi n+\frac{\pi}{3} \text { and }x=2\pi n -\frac{\pi}{3}$ , which we can make into one equation $x=2\pi n \pm \frac{pi}{3}$

In general

$\begin{equation*}cosx=y\end{equation}$

$\begin{equation*}x=2\pi n \pm arccos(y), n\in\mathbb{Z}\end{equation}$

What about the tangent function? Remember tan has a period of $\pi$ .

Solve $tanx=\sqrt{3}$

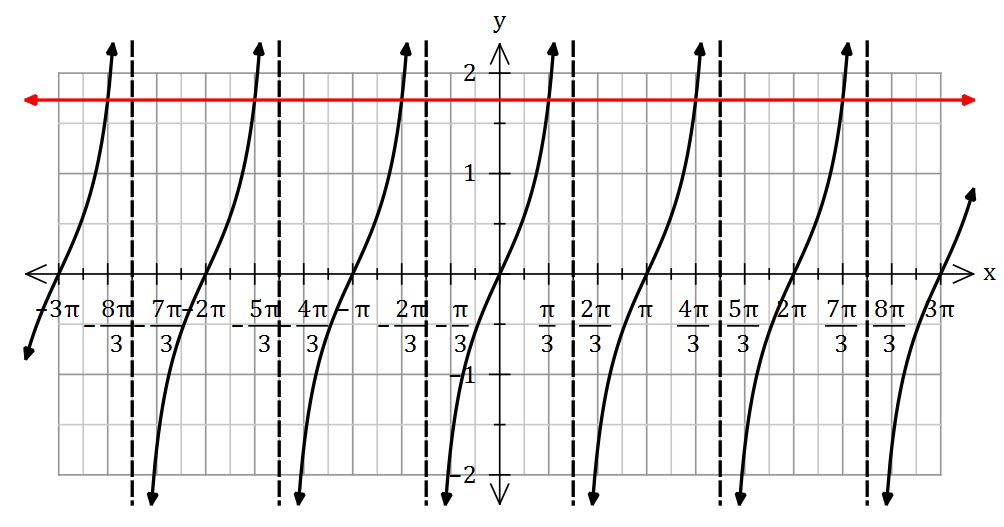
First, note that the solutions are all a common distance ( $\pi$ ) apart.

Tan is positive in the first and the third quadrant

$\begin{equation*}tanx=\sqrt{3}\end{equation}$

$\begin{equation*}x=\frac{\pi}{3} \text { and } x=\pi+\frac{\pi}{3}\end{equation}$

Because all of the solutions are $\pi$ radians apart, the general solution is $x=\frac{\pi}{3} \pm \pi$

In general

$\begin{equation*}tanx=y\end{equation}$

$\begin{equation*}x=arctan(y) + n\pi, n\in \mathbb{Z}\end{equation}$

Examples

Solve for all values of $x$ , $tan^2(x)+tan(x)-6=0$

$\begin{equation*}tan^2(x)+tan(x)-6=0\end{equation}$

This is a quadratic equation – we need two numbers that add to $1$ and multiple to $-6$ , $+3 \text { and } -2$

$\begin{equation*}(tan(x)+3)(tan(x)-2))=0\end{equation}$

$\begin{equation*}tan(x)=-3 \text { or } tan(x)=2\end{equation}$

$\begin{equation*}x=arctan(-3)+n\pi \text { or } x=arctan(2)+n\pi, n\in\mathbb{Z}\end{equation}$

Solve $2cos(2x+\frac{\pi}{18})=\sqrt{3}$

$\begin{equation*}2cos(2x+\frac{\pi}{18})=\sqrt{3}\end{equation}$

$\begin{equation*}cos(2x+\frac{\pi}{18})=\frac{\sqrt{3}}{2}\end{equation}$

$\begin{equation*}2x+\frac{\pi}{18}=2n\pi \pm \frac{\pi}{6}\end{equation}$

$\begin{equation*}2x=2n\pi \pm \frac{\pi}{6}-\frac{\pi}{18}\end{equation}$

$\begin{equation*}2x=2n\pi \pm \frac{\pi}{9}\end{equation}$

$\begin{equation*}x=n\pi \pm \frac{\pi}{18}\end{equation}$

Leave a Comment

Filed under Algebra, Quadratic, Solving Equations, Solving Trig Equations, Trigonometry, Year 11 Specialist Mathematics

Tagged as general solution to trig equations, solving trig equations