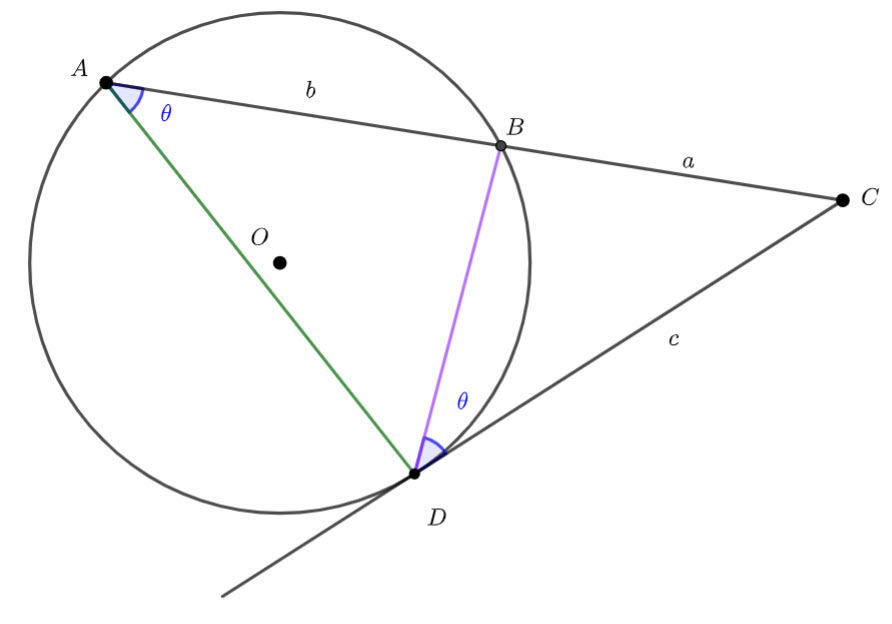
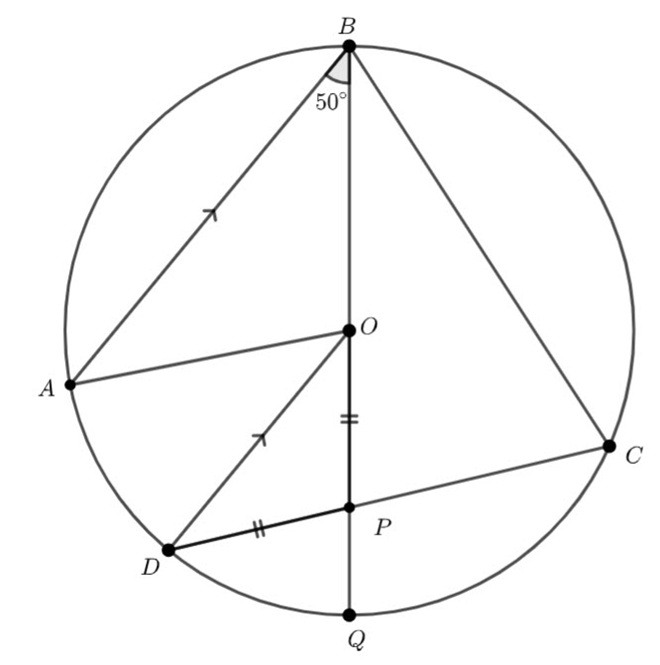
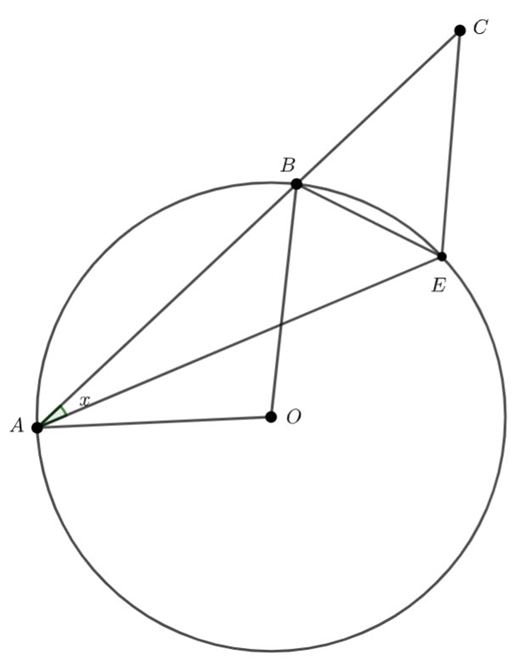
In the diagram, points ![]() and
and ![]() lie on a circle centre
lie on a circle centre ![]() , radius
, radius ![]() cm and diameter
cm and diameter ![]() is parallel to
is parallel to ![]() and point
and point ![]() lies on diameter
lies on diameter ![]() such that
such that ![]() cm.
cm.
(a) Find ![]()
(b) Determine the length of ![]() .
.
![]() (Co-interior angles in parallel lines are supplementary.)
(Co-interior angles in parallel lines are supplementary.)
![]() (Angles subtended by the same arc. The angle at the centre is twice the angle at the circumference.)
(Angles subtended by the same arc. The angle at the centre is twice the angle at the circumference.)
![]()
Let ![]()
From the intersecting chord theorem
![]()
![]()
![]()
![]()
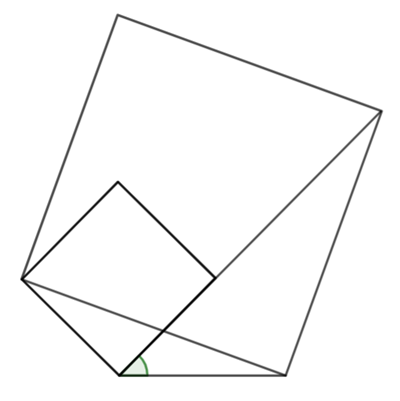
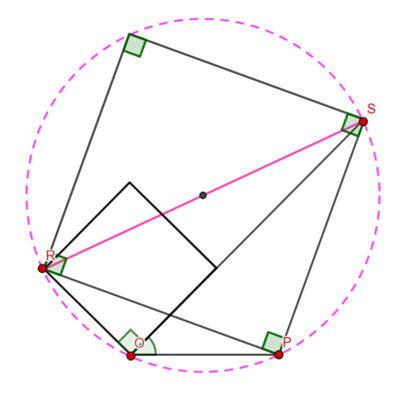
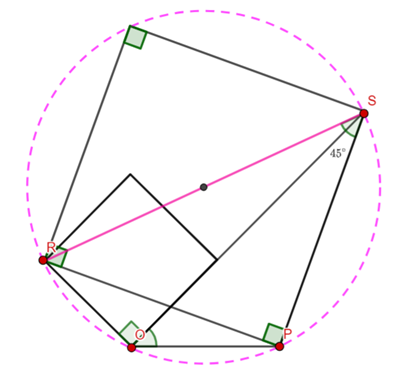
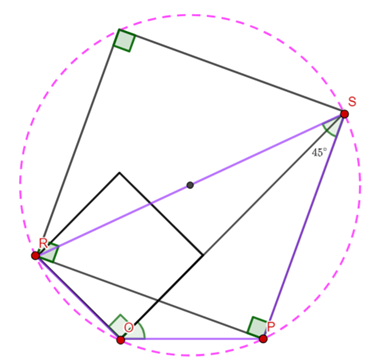
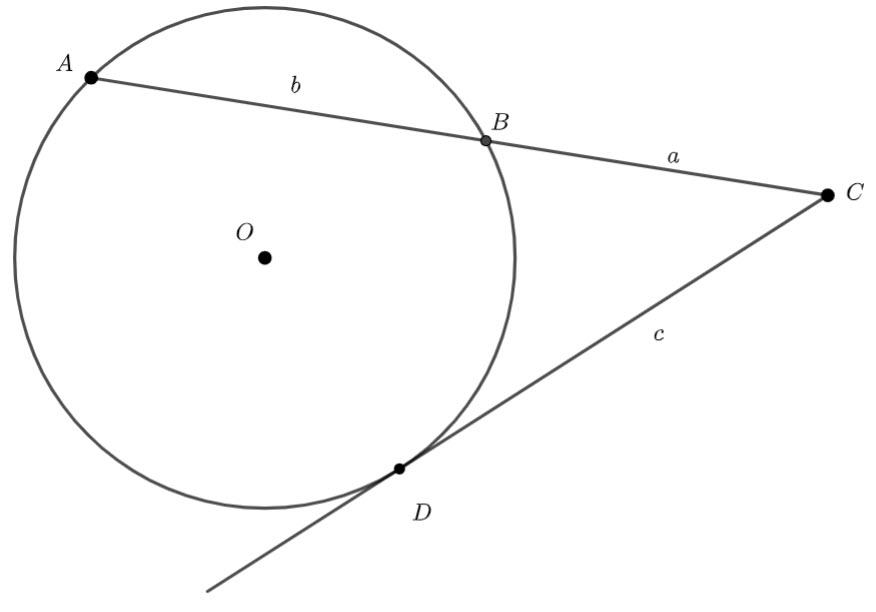
A chord ![]() of a circle
of a circle ![]() is extended to
is extended to ![]() . The straight line bisecting
. The straight line bisecting ![]() meets the circle at
meets the circle at ![]() . Let
. Let ![]() . Prove that
. Prove that ![]() bisects
bisects ![]() .
.
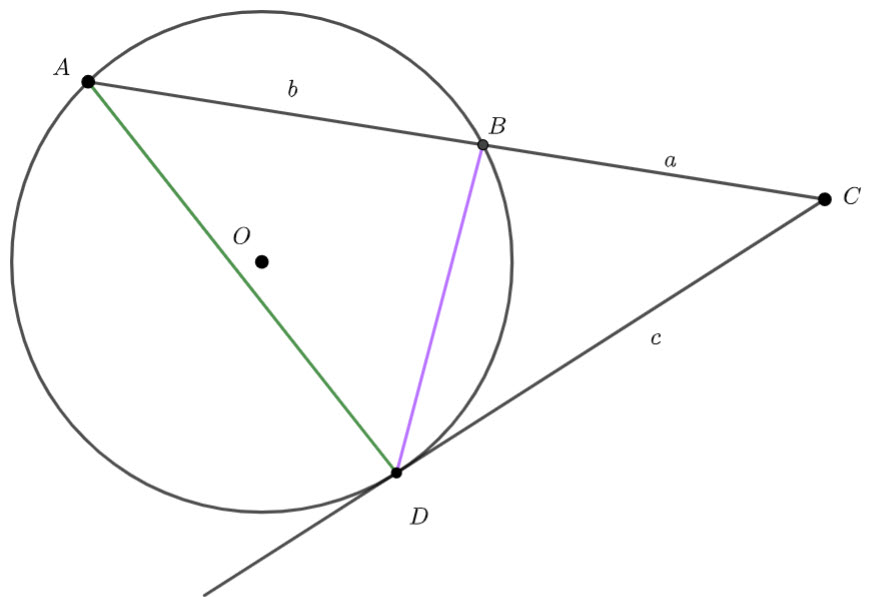
![]() (
(![]() bisects
bisects ![]() )
)
![]() is isosceles (
is isosceles (![]() radii of the circle)
radii of the circle)
![]() (Equal angles in isosceles triangle)
(Equal angles in isosceles triangle)
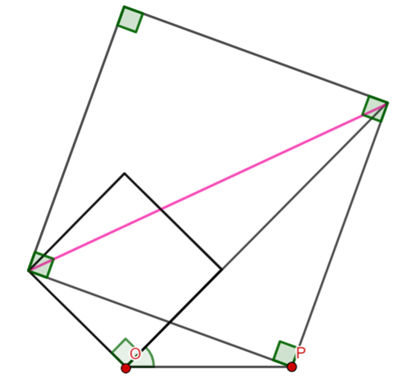
Therefore ![]() (angle sum of a triangle)
(angle sum of a triangle)
![]() (angle at the circumference is half angle at the centre)
(angle at the circumference is half angle at the centre)
![]() (angle sum of a triangle)
(angle sum of a triangle)
![]() (angles on a straight line)
(angles on a straight line)
![]()
![]()
Hence, ![]() bisects
bisects ![]()

 and
and  are added
are added