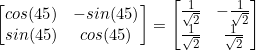The Year 12 Mathematics Methods course doesn’t cover Integration by Parts, so they end up with questions like the following.
Determine the following:
(a)
(b)
Hence, determine the following integral by considering both parts (a) and (b)
(a) Use the product rule
(1) ![]()
(b)
(2) ![]()
I need to use equations ![]() and
and ![]() to find
to find ![]() .
.
The ![]() terms need to vanish and I need
terms need to vanish and I need ![]() of the
of the ![]() terms.
terms.
![]()
(3) ![]()
(4) ![]()
Equation ![]() plus equation
plus equation ![]()
(5) ![]()
Integrate both sides of the equation
![]()
By the fundamental theorem of calculus, we know
![]()
![]()
![]()
Integration by Parts
Remember ![]()
![]()
Let ![]() , then
, then ![]()
and ![]() , then
, then ![]()
![]()
![]()
![]()
Let ![]() , then
, then ![]()
and ![]() . then
. then ![]()
![]()
![]()
![]()
Collect like terms (the integrals are like)
![]()
![]()

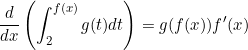
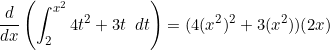
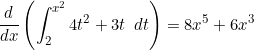
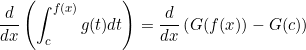











 line)
line)