August 8, 2024 · 5:42 am

Pythagoras Question

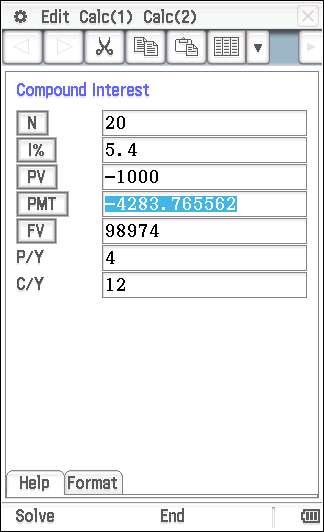
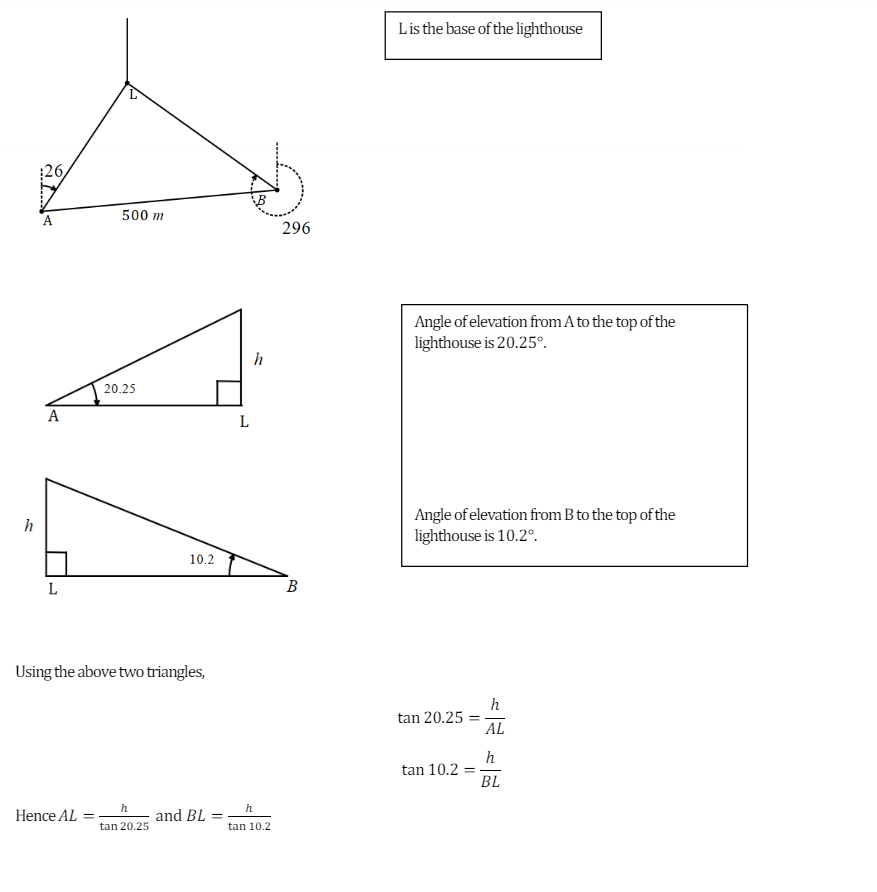
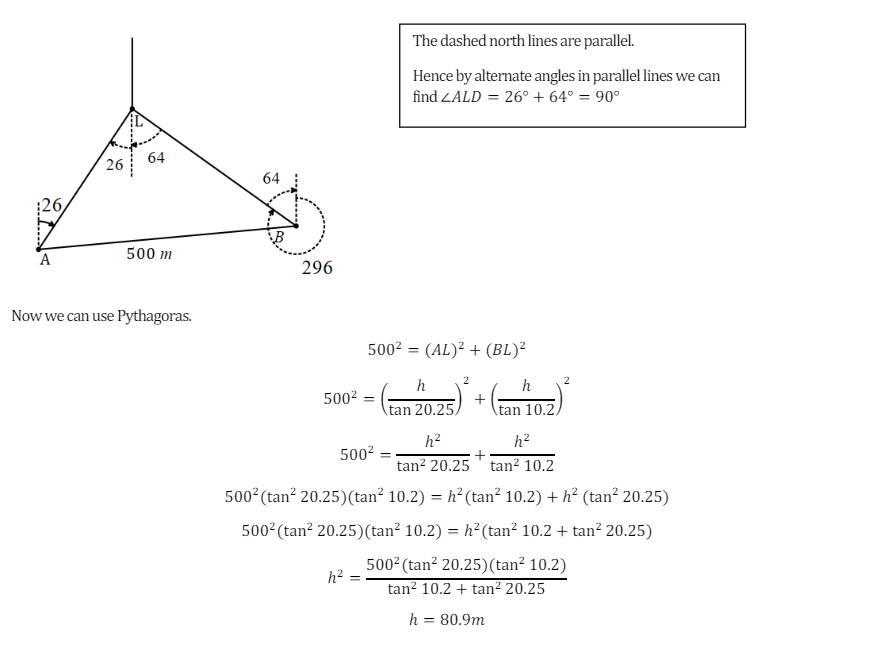
This was a question one of my year 9s had to tackle:

A hemisphere of radius length 5cm is partially filled with water. The top of the hemisphere is horizontal and the surface of the water is a circle of radius 4cm. Find the depth of the water.

ICE-EM Mathematics 9, page 70, question 2

Below is a cross section of the hemisphere

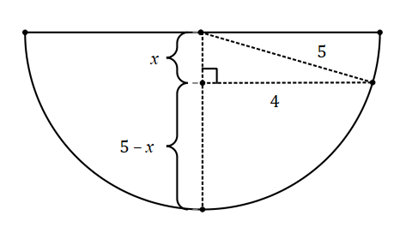
The depth of the water is 5-x

We can find x using the Pythagorean theorem

x^2=5^2-4^2

x=3 (it’s the classic 3-4-5 triangle)

Hence the depth of the water is 2cm.

Leave a Comment

Filed under Pythagoras

Tagged as ,

July 25, 2024 · 7:05 am

Function Composition and Domain and Range

My year 12 Specialist students have been working on function composition and the domain and range of the resulting composition. And they have been struggling a bit with why the composition doesn’t exist.

For example,

The functions f and g are defined by f(x)=x^2-2 and g(x)=\sqrt{x}

(a) Explain why g(f(x)) is not defined.

(b) By suitably restricting the domain of f, obtain a function f_1 such that g(f_1(x))is defined.

For the composite function to exist the range of the inner function (in this case f(x)) must be a subset of the domain of the outer function (in this case g(x)).

Start by finding the domain and range of each function.

f(x)=x^2-2
D_{f(x)}=\{x:x\in\mathbb{R}\}
R_{f(x)}=\{y:y\geq-2,y\in\mathbb{R}\}		g(x)=\sqrt{x}
D_{g(x)}=\{x:x\geq0,x\in\mathbb{R}\}
R_{g(x)}=\{y:y\geq0,y\in\mathbb{R}\}

We can see the range of f(x) is not a subset of the domain of g(x)

i.e. R_{f(x)}\nsubseteq D_{g(x)}

We can restrict the range of f(x) by restricting the domain.

f(x)\geq0

x^2-2\geq0

x^2\geq2

x\leq -\sqrt{2} or x\geq \sqrt{2}

Therefore f_1(x)=x^2-2, x\leq -\sqrt{2} or x\geq \sqrt{2}

and g(f_1(x))=\sqrt{x^2-2}, x\leq -\sqrt{2} or x\geq \sqrt{2}

Leave a Comment

Filed under Composition, Functions

July 16, 2024 · 7:35 am

Australian Mathematics Competition – Polynomial Question

I came across this question from the 2010 Senior Australian Mathematics Competition:

A polynomial f is given. All we know about it is that all its coefficients are non-negative integers, f(1)=6 and f(7)=3438. What is the value of f(3)

Australian Mathematics Competition 2006-2012

I thought ‘excellent, a somewhat hard polynomial question for my students’ and then I tried it. Now I know why only 1% of students got it correct.

As we don’t know the order of the polynomial, let

f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x^1+a_0

We know all of the coefficients are greater than or equal to zero. We also know

f(1)=a_n+a_{n-1}+...+a+a_0=6

Which means that all of the coefficients are between zero and six

0\le{a_n}\le{6}

We have also been given f(7)

f(7)=7^na_n+7^{n-1}a_{n-1}+ ... +7a+1=3438

As all of the coefficients are between zero and six, this is 3438 written in base 7.

Let’s calculate a few powers of 7

Powers of 7
7^01
7^17
7^249
7^3343
7^42401
7^516807
As numbersAs Powers of 7
3438=1\times2401+10373438=1\times7^4+1037
1037=3\times343+81037=3\times7^3+8
8=1\times7+18=1\times7^1+1
1=1\times11=1\times7^0

Hence 3438 written in base 7 is 13011

Therefore f(x)=x^4+3x^3+x+1

f(3)=3^4+3\times3^3+3+1

f(3)=81+81+4

f(3)=166

I really like this question. I think it could work well as a class extension activity with a bit of scaffolding.

Leave a Comment

Filed under Number Bases, Polynomials

Tagged as , ,

June 12, 2024 · 7:37 am

Year 12 Mathematics Applications Finance

Ming, a former high school student and now a successful business owner, wishes to set up a perpetuity of $6000 per year to be paid to a deserving student from her school. The perpetuity is to be paid at the start of the year in one single payment.

(a) A financial institution has agreed to maintain an account for the perpetuity paying a fixed rate of 5.9% p.a. compounded monthly. Show that an amount of $98 974, to the nearest dollar, is required to maintain this perpetuity.

(b) Ming allows herself five years to accumulate the required $98 974 by making regular quarterly payments into an account paying 5.4% p.a. compounded monthly. Determine the quarterly payment needed to reach the required amount after five years if Ming starts the account with an initial deposit of $1000.

SCSA 2017 CA 8

(a) For a perpetuity, we want the interest to equal the payment.

Remember the compound interest formula is

A=P(1+\frac{r}{100n})^{nt}

Where P is the principal, r is the interest rate (as a percent), n is the number of compounding periods in a year, and t is the time.

\therefore I=A-P

I=P(1+\frac{r}{100n})^{nt}-P

6000=P(1.00492)^12-P

P=\frac{6000}{(1.00492^12-1)}

P=98 974.14

Therefore an amount of $98 974 is required to maintain this perpetuity

For part (b) I will use the Finance Solver on a Classpad (Casio).


N is the number of payments, 4\times 5=20

PV is the principal value. To get the signs correct it is
helpful to think about the direction of the flow of the
money. The $1000 is going away from Ming so it is negative.

FV is the future value.

P/Y is the number of payments per year (quarterly so 4)

C/Y is the number of compounding periods per year (monthly so 12).

PMT is the payment

The quarterly payments are $4283.77.

Leave a Comment

Filed under Classpad Skills, Finance, Finance, Year 12 Mathematics Applications

Tagged as

· 7:02 am

The Logistic Equation

My year 12 Specialist students are working on logistic growth at the moment. An example might be helpful.

A new viral disease was found to spread according to the equation \frac{dN}{dt}=kn(M-N), where M is the susceptible population, N is the number of people infected at time t months and k=1.5\times 10^{-9}. In March 2010, it was thought only 100 people out of a population of 18 million were infected. Use the logistic model to find the number infected in:

(a) March 2011

(b) June 2012

(c) January 2017

Specialist 12 – Nelson Senior Maths

\frac{dN}{dt}=kN(M-N)

\frac{dN}{dt}=(1.5\times10^{-9})N(18\times10^{6}-N)

\frac{dN}{N(18\times10^{6}-N)}=1.5\times10^{-9}dt

Use partial fractions to separate the denominator \frac{dN}{N(18\times10^{6}-N)}

\frac{1}{N(18\times10^{6}-N)}=\frac{A}{N}+\frac{B}{18\times10^{6}-N}

1=A(18\times10^{6}-N)+BN

When N=0

1=A(18\times10^{6})

A=\frac{1}{18\times10^{6}}

When N=18\times10^{6}

1=B(18\times10^{6})

B=\frac{1}{18\times10^{6}}

\frac{1}{18\times10^{6}}(\frac{1}{N}+\frac{1}{(18\times10^{6}-N)}dN)=1.5\times10^{-9}dt

\int\frac{1}{N}+\frac{1}{(18\times10^{6}-N)}dN=\int27\times10^{-3}dt

\ln|N|-\ln|18\times10^{6}-N|=(27\times10^{-3})t+c

\ln|\frac{N}{18\times10^{6}-N}|=(27\times10^{-3})t+c

\frac{N}{18\times10^{6}-N}=e^{(27\times10^{-3})t+c}

Let A=e^{c} and rearrange to make N the subject.

N=\frac{(18\times10^{6})Ae^{(27\times10^{-3})t}}{1+Ae^{(27\times10^{-3})t}}

Divide by Ae^{(27\times10^{-3})t}

N=\frac{(18\times10^{6})}{\frac{1}{A}e^{-(27\times10^{-3})t}+1}

Initially 100 people were infected.

100=\frac{(18\times10^{6})}{\frac{1}{A}+1}

A=\frac{1}{179999}

N=\frac{(18\times10^{6})}{179999e^{-(27\times10^{-3})t}+1}

(a) t=12, N=138.3, hence 138

(b) t=27, N=207.3, hence 207

(c) t=82, N=915.2, hence 915.

It is not necessary to solve the differential equation, you can use the formula

\frac{dP}{dt}=rP(k-P)\leftrightarrowP=\frac{kP_0}{P_0+(k-P_0)e^{-rkt}}

This formula is on the Year 12 Mathematics Specialist formula sheet for Western Australia.

For our question,

\frac{dN}{dt}=(1.5\times10^{-9})N(18\times10^6-N)

So, P=\frac{18\times10^{6}\times100}{100+(18\times10^6-100)e^{-(1.5\times10^{-9})(18\times10^6)t}}

And you can substitute values for t.

Leave a Comment

Filed under Differential Equations, Integration, Logistic Growth

Tagged as ,

June 1, 2024 · 7:43 am

Non-Right Trigonometry Problem

I worked on this question with one of my students (I don’t know where it is from).


Mike leaves the rose bush he was examining and walks 35m in the direction
S20^{\circ}W towards a pond.
From there he walks 70m towards a rotunda. Mike is now 100m from the rose bush.
Find the bearing of the rotunda from the pond.

Let’s try to draw a diagram

Because we don’t the direction Mike walked from the pond, I have drawn a circle with radius 70m centred at the pond.

We know Mike is now 100m from the rose bush. As we don’t know the direction, I have drawn another circle with radius 100m centred at the rose bush. Where the two circles intersect are the possible locations of the rotunda.

First Position



Use the cosine rule to find the angle
cos\theta=\frac{b^2+c^2-a^2}{2bc}
cos\theta=\frac{70^2+35^2-100^2}{2(70)(35)}
\theta=cos^{-1}(\frac{-3875}{5250})
\theta=137.6^{\circ}




Using the fact that alternate angles in parallel lines are congruent, we can see
that the bearing from the pond to the rotunda is
360-(137.6-20)=242.2^{\circ} T

Second Position


It is the same triangle, so
\theta=137.6^{\circ}.

This time the bearing is
20+137.6=157.6^{\circ}T

Hence, the two possible bearings of the rotunda from the pond are 242.2^{\circ}T or 157.6^{\circ}T.

Leave a Comment

Filed under Bearings, Non-Right Trigonometry, Trigonometry

Tagged as ,

May 28, 2024 · 6:52 am

Proof of the Sine Rule

As I have done a cosine rule proof, I thought I should also do a sine rule proof.

\frac{sinA}{a}=\frac{sinB}{b}=\frac{sinC}{c}\textnormal{ or }\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}

From the above diagram, we can find h in two ways.

sinC=\frac{h}{a}

(1)   \begin{equation*}h=asinC\end{equation*}

sinA=\frac{h}{c}

(2)   \begin{equation*}h=csinA\end{equation*}

Set equation 1 equal to equation 2

asinC=csinA

\frac{a}{sinA}=\frac{c}{sinC} or \frac{sinC}{c}=\frac{sinA}{a}

We could have put the altitude of the triangle from vertex A

Following the same process as above

sinC=\frac{h}{b}

(3)   \begin{equation*}h=bsinC\end{equation*}

sinB=\frac{h}{c}

(4)   \begin{equation*}h=csinB\end{equation*}

Set equation 3 equal to equation 4.

bsinC=csinB

\frac{b}{sinB}=\frac{c}{sinC}

Now \frac{c}{sinC}=\frac{a}{sinA} therefore

\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA} or \frac{sinB}{b}=\frac{sinC}{c}=\frac{sinA}{a}

Leave a Comment

Filed under Non-Right Trigonometry, Right Trigonometry, Trigonometry

Tagged as , ,

May 26, 2024 · 1:07 pm

Quadratic Rule from a Table of Values

How do you find a quadratic rule from a table of values?

For example,

x1 2 3 4
y061424

Find the first difference

First Difference6-0=614-6=824-14=10

Find the second difference (if the second difference is a constant, then it is quadratic)

Second Difference8-6=2 10-8=2

The general equation of a quadratic is y=ax^2+bx+c

The second difference is 2a

Hence our equation is now y=x^2+bx+c

The c value is the vertical intercept (x=0). We can back track in the table

x01234
yc061424

As the first differences are 6, 8, 10, the one between 0 and 1 must be 4

0-c=4

c=-4

Our equation is now y=x^2+bx-4.

We can now use any other point to find the b value.

Let’s use the point (2, 6)

6=2^2+b(2)-4

6=4-2b-4

6=2b

b=3

The function is y=x^2+3x-4

Let’s try another one

x3456
y7173149

First differences

First difference101418

Second difference

Second Difference44

Hence 2a=4, therefore a=2

The equation is now y=2x^2+bx+c

Instead of back tracking, this time I am going to use two points and simultaneous equations.

Using points (3, 7) and (4, 17)

    \[7=2(3)^2+b(3)+c\]

(1)   \begin{equation*}3b+c=-11\end{equation*}

    \[17=2(4)^2+b(4)+c\]

(2)   \begin{equation*}4b+c=-15\end{equation*}

Equation 2 – Equation 1

b=-4

Substitute b=-4 into equation 1

3(-4)+c=-11

-12+c=-11

c=1

Hence the equation is y=2x^2-4x+1

Leave a Comment

Filed under Quadratics, Uncategorized

Tagged as ,

May 25, 2024 · 7:58 am

Proof of the cosine rule

    \[a^2=b^2+c^2-2bccos(A)\]

From the diagram above

    \[h^2=a^2-(b-x)^2\textnormal{ and }h^2=c^2-x^2\]

    \[\therefore a^2-(b-x)^2=c^2-x^2\]

    \[a^2-(b^2-2bx+x^2)=c^2-x^2\]

    \[a^2-b^2+2bx-x^2-c^2+x^2=0\]

(1)   \begin{equation*}a^2=b^2+c^2-2bx\end{equation*}

From the diagram above, we can see

    \[cos A=\frac{x}{c}\]

(2)   \begin{equation*}x=c cos A\end{equation*}

Substitute equation 2 into equation 1

    \[a^2=b^2+c^2-2bc cosA\]

It can also be handy to have the angle version

    \[cosA=\frac{b^2+c^2-a^2}{2bc}\]

1 Comment

Filed under Non-Right Trigonometry, Right Trigonometry, Trigonometry, Uncategorized

Tagged as ,

May 19, 2024 · 5:42 am

Right-Angled Trigonometry Question (very hard)

One of my year 10 students came with this question from his text book.

ICE_EM Mathematics Year 10 Third Edition

Here is my solution.

A pdf version of the solution

Leave a Comment

Filed under Right Trigonometry, Trigonometry, Uncategorized

Tagged as , ,