Solve ![]() for
for ![]()
Remember the identity
(1) ![]()
Hence
![]()
Now I have
![]()
![]()
![]() or
or ![]()
![]()
![]() for
for ![]()
![]()
![]()
Hence ![]()
Solve ![]() for
for ![]()
Remember the identity
(1) ![]()
Hence
![]()
Now I have
![]()
![]()
![]() or
or ![]()
![]()
![]() for
for ![]()
![]()
![]()
Hence ![]()
In the diagram below, ![]() and
and ![]() lie on the circle with centre
lie on the circle with centre ![]() . If
. If ![]() and
and ![]() , determine with reasoning
, determine with reasoning ![]() and
and ![]()

We know ![]() – radii of the circle.
– radii of the circle.
Which means, ![]() is isosceles and
is isosceles and ![]() – equal angles isosceles triangle.
– equal angles isosceles triangle.
![]() – angle at the centre twice the angle at the circumference.
– angle at the centre twice the angle at the circumference.
![]()

This means ![]() – angles on a straight line are supplementary
– angles on a straight line are supplementary
![]() – equal angles isosceles triangle and the angle sum of a triangle.
– equal angles isosceles triangle and the angle sum of a triangle.
![]() – angle at the circumference subtended by the same arc are congruent.
– angle at the circumference subtended by the same arc are congruent.

![]() – angles at the circumference subtended by the same arc are congruent.
– angles at the circumference subtended by the same arc are congruent.
![]() – equal angle isosceles triangle
– equal angle isosceles triangle
Hence ![]()
Find exactly ![]()
We must be able to find an arithmetic combination of the exact values we knew to find ![]() .
.
![]()
![]()
I re-arranged as above, so I could take advantage of ![]() and
and ![]()
| Useful identities |
![]()
![]()
![]()
![]()
![]()
![]()
Hence,
![]()
![]()
![]()
Use the quadratic equation formula
![]()
![]()
![]()
![]()
![]()
As ![]() ,
, ![]()
My Year 11 Specialist students have had an investigation which involves finding eigenvalues, eigenvectors and lines that are invariant under a particular linear transformation. This is not part of the course, but I feel for teachers who have to create new investigations every year.
Let’s find the eigenvalues and eigenvectors for matrix 
We want to find ![]() such that
such that
(1) ![]()
We solve ![]()

![]()
Hence ![]() and
and ![]()
When ![]() ,
, 
Hence, ![]()
![]() and the eigenvector is
and the eigenvector is ![]()
When ![]() ,
, 
Hence, ![]()
![]() and the eigenvector is
and the eigenvector is ![]()
Which means the invariant lines are ![]() and
and ![]()


 line)
line)
The unit square is rotated about the origin by
anti-clockwise.
(a) Find the matrix of this transformation.
(b) Draw the unit square and its image on the same set of axes.
(c) Find the area of the over lapping region.
Remember the general rotation matrix is
![]()
Hence
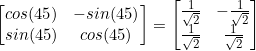
The unit square has co-ordinates
![]()

Transform the unit square



The overlapping area is the area of ![]() – the area of
– the area of ![]()
We know ![]() because the diagonal of a square bisects the angle.
because the diagonal of a square bisects the angle.
We know![]() is a right angle as it’s on a straight line with the vertex of a square.
is a right angle as it’s on a straight line with the vertex of a square.
Hence ![]() is isosceles.
is isosceles.
![]() and
and ![]() , hence
, hence ![]()
![]()
![]()
Area of shaded region =![]()
We are going to find a matrix to rotate a point about the origin a number of degrees (or radians).

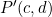

![]() and
and ![]() are equidistant from the origin. I.e.
are equidistant from the origin. I.e. ![]()
Remember, anti-clockwise angles are positive.
![]()
![]()
Use the cosine addition identity.
![]()
![]()
(1) ![]()
We will do the same for ![]()
![]()
![]()
Use the sine addition identity.
![]()
![]()
(2) ![]()
Let ![]() be the rotation matrix, then
be the rotation matrix, then
![]()
Hence ![]() must be
must be
(3) ![]()
Find the image of the line ![]() after it is rotated
after it is rotated ![]() about the origin.
about the origin.
I am going to select two points on the line and transform them.
![]()

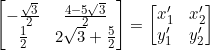
We can then find the equation of the line.
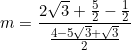
![]()
![]()
![]()

Solve ![]() for
for ![]()
Sine is positive in the first and second quadrants.
![]()
![]()
But what if we aren’t given a domain for the ![]() values?
values?
Then we need to give general solutions.
For example,
Solve ![]()
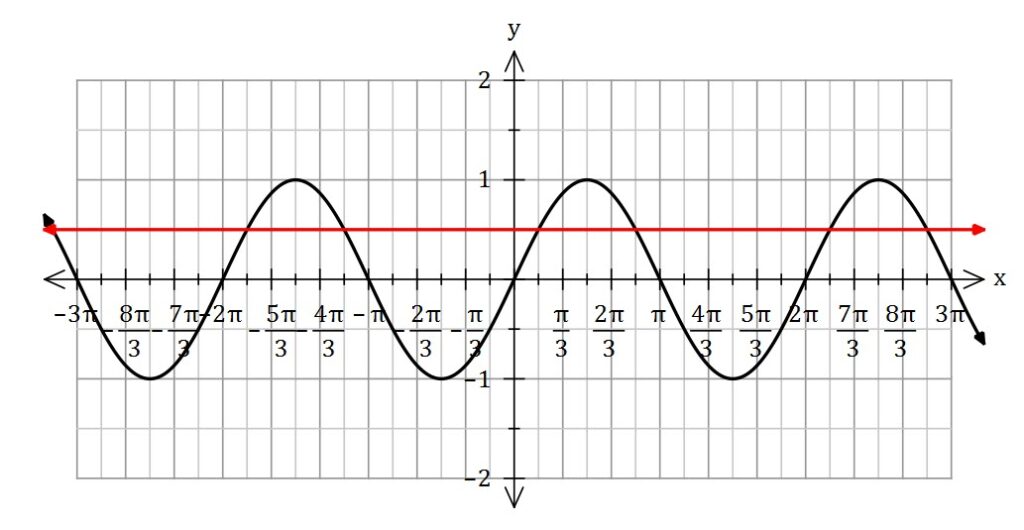
As you can see from the sketch above, there are infinite solutions.
The sine function has a period of ![]() , and so if
, and so if ![]() is a solution then
is a solution then ![]() is also a solution. This means
is also a solution. This means ![]() is a general solution. And we can do the same for the second solution
is a general solution. And we can do the same for the second solution ![]() .
.
In general
We can turn this into one equation
What about cosine?
Solve ![]()
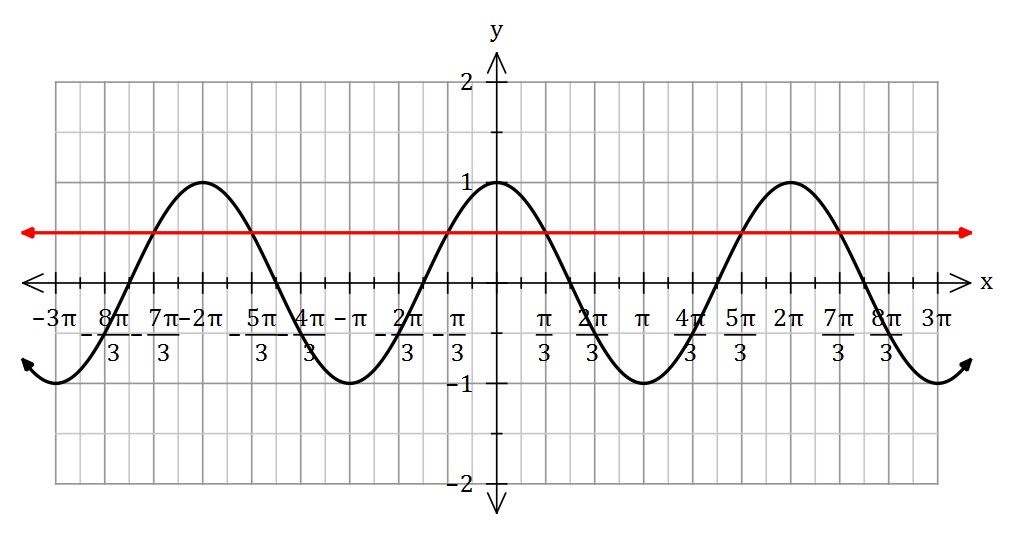
Cosine is positive in the first and fourth quadrants (it also has a period of ![]() . The first two (positive) solutions are
. The first two (positive) solutions are ![]() and
and ![]() .
.
To generalise, ![]() , which we can make into one equation
, which we can make into one equation ![]()
In general
What about the tangent function? Remember tan has a period of ![]() .
.
Solve ![]()
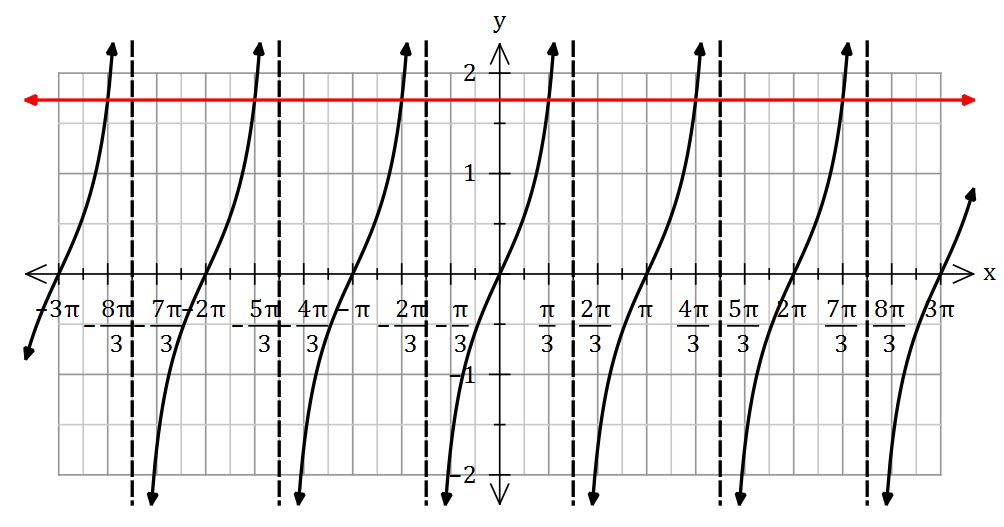
First, note that the solutions are all a common distance (![]() ) apart.
) apart.
Tan is positive in the first and the third quadrant
![]()
![]()
Because all of the solutions are ![]() radians apart, the general solution is
radians apart, the general solution is ![]()
In general
Solve for all values of ![]() ,
, ![]()
![]()
This is a quadratic equation – we need two numbers that add to ![]() and multiple to
and multiple to ![]() ,
, ![]()
![]()
![]()
![]()
Solve ![]()
![]()
![]()
![]()
![]()
![]()
![]()
The easiest approach is to jump right in with some examples.
Example 1
Convert ![]() to a fraction.
to a fraction.
Let
(1)
(2)
Subtract equation
from equation
Hence
so
Example 2
Convert ![]() to a fraction.
to a fraction.
Let
(3)
(4)
Subtract equation
from equation
.
Example 3
Convert ![]() to a fraction
to a fraction
Let
(5)
(6)
(7)
Subtract equation
from equation
Our aim is to manipulate the recurring decimal to create two numbers each which have only the repeated digits after the decimal point.
One more example.
Example 4
Convert ![]() to a fraction
to a fraction
Let ![]()
If I multiply by 10, then I will have ![]() – only repeated digits after the decimal point.
– only repeated digits after the decimal point.
If I multiply by 1000, then I will have ![]() – only repeated digits after the decimal point.
– only repeated digits after the decimal point.
So I get,
![]()
![]()
You can also use your Casio classpad to do the conversion. Although I think it is easier just to do it yourself.
Let’s think about example 4,
![]()
Which is
![]()
![]()

Filed under Arithmetic, Decimals, Fractions, Year 11 Specialist Mathematics