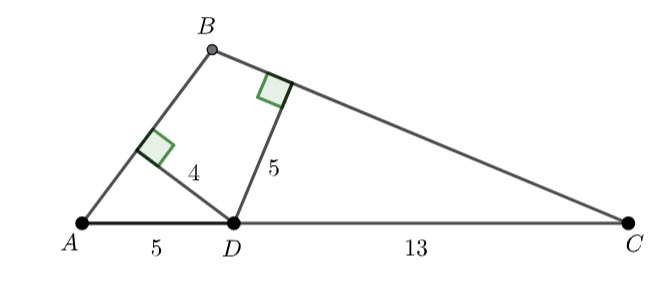
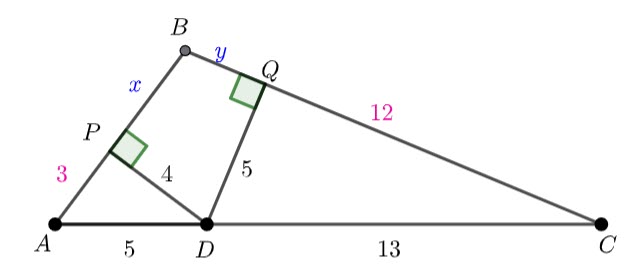
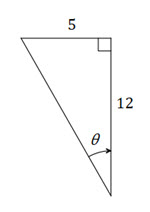
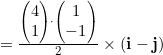I don’t know where I found this question, but it does require algebra and problem solving (as well as right trig and Pythagoras)
From a point ![]() , a lighthouse is on a bearing of
, a lighthouse is on a bearing of ![]() T and the top of the light house is at an angle of elevation of
T and the top of the light house is at an angle of elevation of ![]() . From a point
. From a point ![]() , the lighthouse is on a bearing of
, the lighthouse is on a bearing of ![]() T and the top of the lighthouse is at angle of elevation of
T and the top of the lighthouse is at angle of elevation of ![]() . If
. If ![]() and
and ![]() are 500 metres apart, find the height of the lighthouse.
are 500 metres apart, find the height of the lighthouse.
Let’s draw a diagram.

Let the height of the lighthouse be ![]()

We can find the angle between ![]() , the lighthouse, and
, the lighthouse, and ![]() by using the base triangle
by using the base triangle
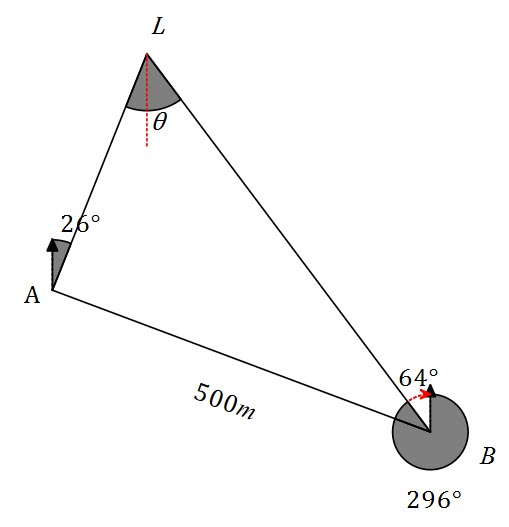
The red line from ![]() is parallel to the two north lines. Hence
is parallel to the two north lines. Hence ![]() (Alternate angles in parallel lines are congruent)
(Alternate angles in parallel lines are congruent)
It’s a right triangle so we know
(1) ![]()
We are going to use the other two triangles to find ![]() and
and ![]()
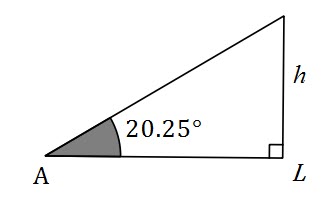 | 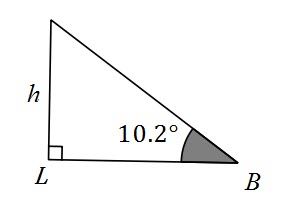 |
Substitute ![]() and
and ![]() into equation
into equation ![]()
![]()
Solve for ![]() .
.
![]()
![]()
![]()