We have seen how the formula for mean (expected value) was derived, and now we are going to look at variance.
In general variance of a probability distribution is
(1) ![]()
We are going to start by calculating ![]()
![]()
![]()
![]()
The ![]() cancels with the
cancels with the ![]() to leave
to leave ![]() on the numerator and
on the numerator and ![]() on the denominator.
on the denominator.
Also, when ![]() and we can start the sum at
and we can start the sum at ![]()
![]()
Let ![]() and
and ![]() , when
, when ![]() and hence
and hence ![]() and when
and when ![]()
Our equation is now
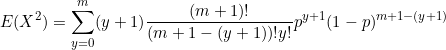
Simplify
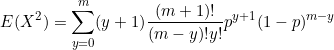
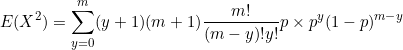
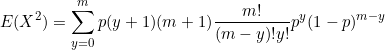
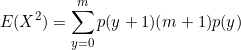
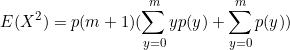
![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now from equation ![]()
![]()
![]()
![]()
(2) ![]()
and the standard deviation is
(3) ![]()
