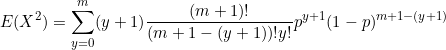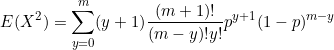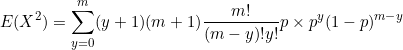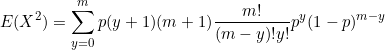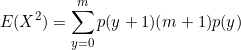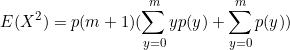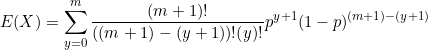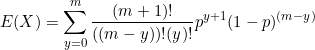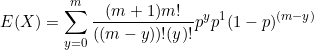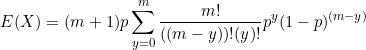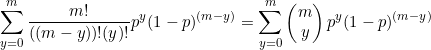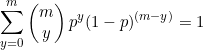Category Archives: Probability Distributions

July 22, 2025 · 6:43 am

Continuous Uniform Random Variable

My Year 12 Mathematics Methods students are doing continuous random variables at the moment and I thought it would be worthwhile deriving the mean and variance formulas for a uniform continuous random variable.

The probability density function for a uniform random variable is

    \begin{equation*}f(x)= \left \{ {\begin{matrix}\frac{1}{b-a} & a\le x\le b \\0 & \text {elsewhere}\end{matrix}}\end{equation}

and it looks like

Remember, the mean \mu or expected value E(X) of a continuous random variable is

(1)   \begin{equation*}E(X)=\int xp(x) dx\end{equation*}

and the variance \sigma^2 is

(2)   \begin{equation*}\sigma^2=\int (x-\mu)^2p(x) dx\end{equation*}

We are going to use equations 1 and 2 to find formulae for a uniform continuous random variable.

    \begin{equation*}\mu=\int_a^b x (\frac{1}{b-a}) dx\end{equation}

    \begin{equation*}\mu=\frac{x^2}{2(b-a)}|\begin{matrix}b\\a\end{matrix}\end{equation}

    \begin{equation*}\mu=\frac{b^2}{2(b-a)}-\frac{a^2}{2(b-a)}=\frac{b^2-a^2}{2(b-a)}\end{equation}

Factorise the numerator (using difference of squares)

    \begin{equation*}\mu=\frac{(b-a)(b+a)}{2(b-a)}\end{equation}

Hence,

    \begin{equation*}\mu=\frac{b+a}{2}\end{equation}

Now for the variance

    \begin{equation*}\sigma^2=\int_a^b (x-(\frac{a+b}{2}))^2(\frac{1}{b-a}) dx\end{equation}

    \begin{equation*}\sigma^2=\frac{1}{b-a}(\frac{(x-\frac{a+b}{2})^3}{3})|\begin{matrix}b\\a\end{matrix}\end{equation}

    \begin{equation*}\sigma^2=\frac{1}{b-a}((\frac{(b-\frac{a+b}{2})^3}{3})-(\frac{(a-\frac{a+b}{2})^3}{3}))\end{equation}

    \begin{equation*}\sigma^2=\frac{1}{b-a}(\frac{-a^3}{12}+\frac{b^3}{12}+\frac{a^2b}{4}-\frac{ab^2}{4})\end{equation}

    \begin{equation*}\sigma^2=\frac{1}{b-a}(\frac{-a^3+b^3+3a^2b-3ab^2}{12})\end{equation}

    \begin{equation*}\sigma^2=\frac{1}{b-a}(\frac{b^3-3b^2a+3ba^2-a^3}{12})\end{equation}

From the binomial expansion theorem, we know

    \begin{equation*}b^3-3b^2a+3ba^2-a^3=(b-a)^3\end{equation}

Hence

    \begin{equation*}\sigma^2=\frac{1}{b-a}(\frac{(b-a)^3}{12}\end{equation}

and

    \begin{equation*}\sigma^2=\frac{(b-a)^2}{12}\end{equation}

Leave a Comment

Filed under Binomial Expansion Theorem, Continuous Random Variables, Probability Distributions, Uniform, Year 12 Mathematical Methods

Tagged as , ,

April 16, 2025 · 8:26 am

Binomial Expansion – deriving the formula for Variance

We have seen how the formula for mean (expected value) was derived, and now we are going to look at variance.

In general variance of a probability distribution is

(1)   \begin{equation*} Var(X)=E(X^2)-(E(X))^2\end{equation*}

We are going to start by calculating E(X^2)

    \begin{equation*}E(X^2)=\sum_{x=0}^nx^2p(x)\end{equation}

    \begin{equation*}E(X^2)=\sum_{x=0}^nx^2\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\end{equation}

    \begin{equation*}E(X^2)=\sum_{x=0}^n x^2\frac{n!}{(n-x)!x!}p^x(1-p)^{n-x}\end{equation}

The x^2 cancels with the x! to leave x on the numerator and (x-1)! on the denominator.

Also, when x=0, x^2=0 and we can start the sum at x=1

    \begin{equation*}E(X^2)=\sum_{x=1}^n x\frac{n!}{(n-x)!(x-1)}!p^x(1-p)^{n-x}\end{equation}

Let y=x-1 and m=n-1, when x=n, y=n-1 and hence y=m and when x=1, y=0

Our equation is now

    \begin{equation*}E(X^2)=\sum_{y=0}^m (y+1)\frac{(m+1)!}{(m+1-(y+1))!y!}p^{y+1}(1-p)^{m+1-(y+1)}\end{equation}

Simplify

    \begin{equation*}E(X^2)=\sum_{y=0}^m(y+1)\frac{(m+1)!}{(m-y)!y!}p^{y+1}(1-p)^{m-y}\end{equation}

    \begin{equation*}E(X^2)=\sum_{y=0}^m(y+1)(m+1)\frac{m!}{(m-y)!y!}p\times p^y(1-p)^{m-y}\end{equation}

    \begin{equation*}E(X^2)=\sum_{y=0}^m p(y+1)(m+1)\frac{m!}{(m-y)!y!} p^y(1-p)^{m-y}\end{equation}

    \begin{equation*}E(X^2)=\sum_{y=0}^m p(y+1)(m+1)p(y)\end{equation}

    \begin{equation*}E(X^2)=p(m+1)(\sum_{y=0}^myp(y)+\sum_{y=0}^mp(y))\end{equation}

\sum_{y=0}^mp(y)=1 and \sum_{y=0}^myp(y)=E(Y)

    \begin{equation*}E(X^2)=p(m+1)(E(Y)+1)\end{equation}

E(Y)=mp

    \begin{equation*}E(X^2)=p(m+1)(mp+1)\end{equation}

m+1=n

    \begin{equation*}E(X^2)=pn((n-1)p+1)\end{equation}

    \begin{equation*}E(X^2)=n^2p^2-np^2+np\end{equation}

Now from equation 1

    \begin{equation*}Var(X)=E(X^2))-(E(X))^2\end{equation}

    \begin{equation*}=Var(X)=n^2p^2-np^2+np-n^2p^2\end{equation}

    \begin{equation*}Var(X)=-np^2+np\end{equation}

(2)   \begin{equation*}Var(X)=np(1-p)\end{equation*}

and the standard deviation is

(3)   \begin{equation*}\sigma_X=\sqrt{np(1-p)}\end{equation*}

1 Comment

Filed under Algebra, Binomial, Probability Distributions, Standard Deviation

Tagged as , ,

April 13, 2025 · 9:23 am

Binomial Distribution – deriving the equation for mean (expected value)

The mean, \mu of a binomial distribution is

(1)   \begin{equation*}\mu=np\end{equation*}

where n is the number of trials and p is the probability of success.

For any discrete probability distribution , the expected value or mean is

(2)   \begin{equation*}E(X)=\sum_{x=0}^nxp(x)\end{equation*}

For example, if a coin is tossed 3 times and the number of heads is recorded, the distribution is

X0123
P(X=x)\frac{1}{8}\frac{3}{8}\frac{3}{8}\frac{1}{8}

    \begin{equation*}E(X)=0\times\frac{1}{8}+1\times\frac{3}{8}+2\times\frac{3}{8}+3\times{1}{8}\end{equation}

    \begin{equation*}E(X)=\frac{12}{8}=\frac{3}{2}\end{equation}

I want to show how the \mu=np formula is derived from the general formula (equation (2)).

    \begin{equation*}E(X)=\sum^n_{x=0}xp(x)\end{equation}

For a binomial distribution, p(x)=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}

    \begin{equation*}E(X)=\sum_{x=0}^nx\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\end{equation}

    \begin{equation*}E(X)=\sum^n_{x=0}x\frac{n!}{(n-x)!x!}p^x(1-p)^{n-x}\end{equation}

The x can cancel with the x! to leave (x-1)! on the denominator.

    \begin{equation*}E(X)=\sum^n_{x=0}\frac{n!}{(n-x)!(x-1)!}p^x(1-p)^{n-x}\end{equation}

Also, when x=0 \Rightarrow xp(x)=0, hence the sum can start at x=1.

    \begin{equation*}E(X)=\sum^n_{x=1}\frac{n!}{(n-x)!(x-1)!}p^x(1-p)^{n-x}\end{equation}

Let y=x-1 and m=n-1

When x=n \Rightarrow y=n+1=m

    \begin{equation*}E(X)=\sum^{m}_{y=0}\frac{(m+1)!}{((m+1)-(y+1))!(y)!}p^{y+1}(1-p)^{(m+1)-(y+1)}\end{equation}

Simplify

    \begin{equation*}E(X)=\sum^{m}_{y=0}\frac{(m+1)!}{((m-y))!(y)!}p^{y+1}(1-p)^{(m-y)}\end{equation}

    \begin{equation*}E(X)=\sum^{m}_{y=0}\frac{(m+1)m!}{((m-y))!(y)!}p^yp^1(1-p)^{(m-y)}\end{equation}

We can move (m+1) and p out of the sum.

    \begin{equation*}E(X)=(m+1)p\sum^{m}_{y=0}\frac{m!}{((m-y))!(y)!}p^y(1-p)^{(m-y)}\end{equation}

    \begin{equation*}\sum^{m}_{y=0}\frac{m!}{((m-y))!(y)!}p^y(1-p)^{(m-y)}=\sum^{m}_{y=0}\begin{pmatrix}m\\y\end{pmatrix}p^y(1-p)^{(m-y)}\end{equation}

    \begin{equation*}\sum^{m}_{y=0}\begin{pmatrix}m\\y\end{pmatrix}p^y(1-p)^{(m-y)}=1\end{equation}

As it is the sum of the probabilities of a binomial distribution with m trials.

Hence E(X)=(m+1)p=np

Next, deriving the variance formula for a binomial distribution.

1 Comment

Filed under Binomial, Mean, Probability Distributions

Tagged as , ,