Category Archives: Factorising

November 22, 2025 · 6:10 am

Polynomial Long Division

I usually choose to use synthetic division when factorising polynomials, but I know some teachers are unhappy when their students do this. So for completeness, here is my PDF for Polynomial Long Division.

Polynomial Long Division Download

Simultaneous Equation (or is it?)

Solve simultaneously

$X+Y+Z=10$
$XYZ=30$
$XY+YZ+XZ=31$

We could attempt to solve this simultaneously, but I think the algebra would be tricky.

The three equations are related to the roots of a cubic polynomial.

If the general equation of the polynomial is $ax^3+bx^2+cx+d$ , then we know

The sum of the roots

The product of the roots

and

\alpha\beta+\alpha\gamma+\beta\gamma=\frac{c}{a}

So from our three equations we have

(1) $\begin{equation*}X+Y+Z=10=\frac{-b}{a}\end{equation*}$

(2) $\begin{equation*}XYZ=30=\frac{-d}{a}\end{equation*}$

(3) $\begin{equation*}XY+YZ+XZ=31=\frac{c}{a}\end{equation*}$

Let $a=1$ , then $b=-10, c=31$ , and $d=-30$

Our cubic is $t^3-10t^2+31t-30$ and we can try to solve it.

The roots will be factors of $-30$ , so $\pm 1, \pm 2, \pm 3, \pm 5, \pm 6, \pm 10, \pm 15, \pm 30$

Try $t=2$

$\begin{equation*}(2)^3-10(2)^2+31(2)-30=0\end{equation}$

Hence $t=2$ is a root.

Use synthetic division to find the quadratic factor

$2$	$1$	$-10$	$31$	$-30$
		$2$	$-16$	$30$
	$1$	$-8$	$15$	$0$

The quadratic factor is $x^2-8x+15$ , which factorises to $(x-3)(x-5)$

Hence the solutions are $X=2, Y=3$ , and $Z=5$

We could assume the solutions are natural numbers, then we can look at factors of 30.

Hence the solutions are $X=2, Y=3,$ and $Z=5$

But with this approach we might not be able to find the solutions.

Synthetic Division (for factorising and/or solving polynomials)

I use synthetic division to factorise polynomials with a degree greater than 2. For example, $f(x)=x^3+2x^2-5x-6$

It works best with monic polynomials but can be adapted to non-monic ones (see example below).

The only problem is that you need to find a root to start.

Try the factors of $-6$ i.e. $(-1, 1, 2, -2, 3, -3, 6, -6)$

$f(-1)=(-1)^3+2(-1)^2-5(-1)-6=0$

Hence, $x=-1$ is a root and $(x+1)$ is a factor of the polynomial.

Set up as follows

Bring the first number down

Multiply by the root and place under the second co-efficient

Add down

Repeat the process

The numbers at the bottom $(1, 1, -6)$ are the coefficients of the polynomial factor.

We now know $x^3+2x^2-5x-6=(x+1)(x^2+x-6)$ .

We can factorise the quadratic in the usual way.

$x^2+x-6=(x+3)(x-2)$

Hence $x^3+2x^2-5x-6=(x+1)(x+3)(x-2)$ .

Let’s try a non-monic example

Factorise $6x^4+39x^3+91x^2+89x+30$

I know $-2$ is a root. Otherwise I would try the factors of 30.

Use synthetic division

Because this was non-monic we need to divide our new co-efficients $(6, 27, 37, 15)$ by 6 (the co-efficient of the $x^4$ term)

$x^3+\frac{9}{2}x^2+\frac{37}{6}+\frac{5}{2}$

We now need to go again. I know that $\frac{-3}{2}$ is a root and $(2x+3)$ is a factor.

Our quadratic factor is $x^2+3x+5/3$ , which is $3x^2+9x+5$ .

The quadratic factor doesn’t have integer factors so,

$6x^4+39x^3+91x^2+89x+30=(x+2)(2x+3)(3x^2+9x+5)$

I think this is much quicker than polynomial long division.

1 Comment

Filed under Algebra, Factorising, Factorising, Fractions, Polynomials, Quadratic, Simplifying fractions, Solving Equations

Tagged as non monic synthetic division, Synthetic division

April 30, 2025 · 6:08 am

Factorising Non-Monic Quadratics

The general equation of a quadratic is $ax^2+bx+c$

Let’s explore different methods of factorising a non-monic quadratic (the $a$ term is not $1$ )

Factorise $6x^2+x-12$

We need to find two numbers that add to $1$ and multiply to $-72$ (i.e. add to $b$ and multiply to $a\times c)$

The two numbers are $9$ and $-8$

Method 1 – Splitting the middle term

This is the method I teach the most often

$\begin{equation*}6x^2+x-12\end{equation}$

Split the middle term (the $b$ term) into the two numbers

$\begin{equation*}6x^2-8x+9x-12\end{equation}$

The order doesn’t matter.

Find a common factor for the first term terms, and then for the last two terms.

$\begin{equation*}2x(3x-4)+3(3x-4)\end{equation}$

There is a common factor of $(3x-4)$ , factor it out.

$\begin{equation*}(3x-4)(2x+3)\end{equation}$

Method two – Fraction

$\begin{equation*}6x^2+x-12\end{equation}$

Put $6x$ into both factors and divide by $6$

$\begin{equation*}\frac{(6x-8)(6x+9)}{6}\end{equation}$

Factorise

$\begin{equation*}\frac{2(3x-4)3(2x+3)}{6}\end{equation}$

$\begin{equation*}\frac{6(3x-4)(2x+3)}{6}\end{equation}$

$\begin{equation*}(3x-4)(2x+3)\end{equation}$

Method 3 – Monic to non-monic

$\begin{equation*}y=6x^2+x-12\end{equation}$

Multiply both sides of the equation by $a$

$\begin{equation*}6y=6(6x^2+x-12)\end{equation}$

$\begin{equation*}6y=6^2x^2+6x-72\end{equation}$

$\begin{equation*}6y=(6x)^2+6x-72\end{equation}$

Let $A=6x$

$\begin{equation*}6y=A^2+A-72\end{equation}$

Factorise

$\begin{equation*}6y=(A+9)(A-8)\end{equation}$

Replace the $A$ with $6x$

$\begin{equation*}6y=(6x+9)(6x-8)\end{equation}$

$\begin{equation*}6y=3(2x+3)2(3x-4)\end{equation}$

$\begin{equation*}6y=6(2x+3)(3x-4)\end{equation}$

$\begin{equation*}y=(2x+3)(3x-4)\end{equation}$

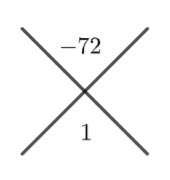
Method 4 – Cross Method

$\begin{equation*}6x^2+x-12\end{equation}$

Place the two numbers in the cross

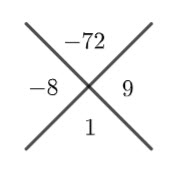
Place the two numbers that add to $1$ and multiply to $-72$ in the other parts of the cross.

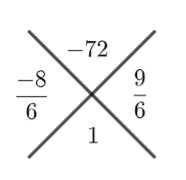
Divide these two numbers by $6$ (i.e $a$ )

Simplify

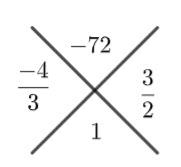
Hence,

$\begin{equation*}(x-\frac{4}{3})(x+\frac{3}{2})\end{equation}$

Which is

$\begin{equation*}(3x-4)(2x+3)\end{equation}$

Method 5 – By Inspection

This is my least favourite method – although students get better with practice

$\begin{equation*}6x^2+x-12\end{equation}$

The factors of $a$ are $1, 2, 3,$ and $6$ and the factors of $12$ are $1, 2, 3, 4, 6, 12$

We know one number is positive and one number negative.

Which give us all of these possibilities

$\begin{equation*}(2x+3)(3x-4)\end{equation}$

With a bit of practice you don’t need to check all of the possibilties, but I find students struggle with this method.

Method 6 – Grid

$\begin{equation*}6x^2+x-12\end{equation}$

Create a grid like the one below


	$6x^2$
		$-12$

Find the two numbers that multiply to $-72$ and add to $1$ and place them in the other grid spots (see below)


	$6x^2$	$-8x$
	$9x$	$-12$

Find the HCF (highest common factor) of each row and put in the first column.

Row $1$ HCF= $2x$ , Row $2$ HCF= $3$


$2x$	$6x^2$	$-8x$
$3$	$9x$	$-12$

For the columns, calculate what is required to multiple the HCF to get the table entry.

For example, what do you need to multiple $2x$ and $3$ by to get $6x^2$ and $9x$ ? In this case it is $3x$ . It’s always going to be the same thing, so just use one value to calculate it,

	$3x$	$-4$
$2x$	$6x^2$	$-8x$
$3$	$9x$	$-12$

The factors are column $1$ and row $1$
$(2x+3)(3x-4)$

The two methods I use the most are splitting the middle term, and the cross method, but I can see value in the grid method.

Infinite Product Expansion of cos (x)

Remember

(1) $\begin{equation*}cos(x)=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+...\end{equation*}$

We know that $cos(x)=0$ for odd integer multiples of $\frac{\pi}{2}$ , i.e. $\frac{\pi}{2}, \frac{3\pi}{2}, ...$ , which is $\frac{(2n-1)\pi}{2}$ for $n\neq 0$

Hence,

$\begin{equation*}0=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+...\end{equation}$

for $x=\frac{(2n-1)\pi}{2}, n>0$

We can factorise our $cos(x)$ expansion

$\begin{equation*}(1-\frac{x^2}{r_1})(1-\frac{x^2}{r_2})...\end{equation}$

We know $r_1=\frac{\pi}{2}, r_2=\frac{3\pi}{2}, ...$

$\begin{equation*}cos(x)=(1-\frac{x^2}{(\frac{\pi}{2})^2})(1-\frac{x^2}{(\frac{3\pi}{2})^2})...(1-\frac{x^2}{(\frac{(2n-1)\pi}{2})^2})\end{equation}$

$\begin{equation*}cos(x)=\Pi_{n=1}^{\infty}(1-\frac{x^2}{(\frac{(2n-1)\pi}{2})^2})\end{equation}$

$\begin{equation*}cos(x)=\Pi_{n=1}^{\infty}(1-\frac{4x^2}{(2n-1)^2\pi^2})\end{equation}$

1 Comment

Filed under Factorising, Identities, Infinite Product Expansion, Interesting Mathematics, Polynomials, Trigonometry

Tagged as infinite product expansion of cos(x), trigonometry

September 19, 2024 · 9:43 am

Solving Cubic Functions

I have been thinking about cubics a bit lately because some of my students are solving and then sketching cubics. Plus I am reading An Imaginary Tale by Paul Nahin, which talks about solving cubics and complex numbers.

Cubics must have at least one real root. If one of the roots is a rational number, then we can use the Factor and Remainder Theorem.

For example,

Solve $2x^3-3x^2-3x+2=0$

But what if it is not factorisable?

For example,

Solve $2x^3+5x^2-2x+4=0$

How many roots does this equation have?

We could find the derivative and find out how many stationary points the function has.

$f'(x)=6x^2+10x-2$

This is a quadratic function. Find the discriminant to determine the number of roots.

$\Delta=b^2-4ac=100-4(6)(-2)=148$

As $\Delta>0$ , there are two stationary points, which means we could have 1, 2 (one root is repeated) or three roots, depending on if the function crosses the $x-$ axis between stationary points. So not much use.

We could try the discriminant of a cubic.

$\Delta=18abcd-4b^3d+b^2c^2-4ac^2-27a^2d^2$

$\Delta=18(2)(5)(-2)(4)-4(5^3)(4)+(5^2)(-2)^2-4(2)(-2)^2-27(2)^2(4)^2=-5100$

The discriminant is negative so there is one real root.

From my reading, we need to turn the cubic into a depressed cubic (cubics of the form $x^3+px+q=0$ ).

We can do this by using a change of variable.

We can then use Cardano’s formula

$x=\sqrt[3]{-\frac{q}{2}+\sqrt{(-\frac{q}{2})^2+(\frac{p}{3})^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{(-\frac{q}{2})^2+(\frac{p}{3})^3}}$

$p=-\frac{37}{12}$ and $q=\frac{431}{108}$
$\frac{p}{3}=\frac{-37}{36}$
$\frac{q}{2}=\frac{431}{216}$
$(\frac{431}{216})^2+(\frac{-37}{36})^3=\frac{139}{48}$
$t=\sqrt[3]{\frac{-431}{216}+\sqrt{\frac{139}{48}}}+\sqrt[3]{\frac{-431}{216}-\sqrt{\frac{139}{48}}}$
$t=-2.21095...$
$\therefore x=-2.21095...-\frac{5}{6}=-3.044$

We can see from the sketch below that there is only one solution and it is about $-3$ .

1 Comment

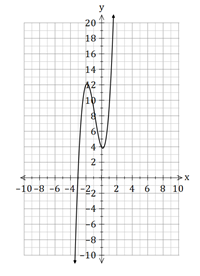
Filed under Cubics, Factorising, Polynomials, Solving

Tagged as Cardano, Cubics, Depressed Cubic, Factorising, Polynomials, Solving

Factors of Thirty	$X+Y+Z$	$XY+YZ+XZ$
$1, 1, 30$	$1+1+30=32$	$1+30+30=61$
$1, 2, 15$	$1+2+15=18$	$2+15+30=47$
$1, 5, 6$	$1+5+6=12$	$5+6+30=41$
$2, 3, 5$	$2+3+5=10$	$6+10+15=31$

Possible factorisations	$b$ term of expansion
$(x-1)(6x+12)$	$12x-6x=6x$	No
$(x-2)(6x+6)$	$6x-12x=-6x$	No
$(x-3)(6x+4)$	$4x-18x-14x$	No
$(2x-1)(3x+12)$	$24x-3x=21x$	No
$(2x-2)(3x+6)$	$12x-6x=6x$	No
$(2x-3)(3x+4)$	$8x-9x=-1x$	Almost, switch the signs
$(2x+3)((3x-4)$	$-8x+9x=1x$	Yes

Category Archives: Factorising

Polynomial Long Division

Simultaneous Equation (or is it?)

Synthetic Division (for factorising and/or solving polynomials)

Factorising Non-Monic Quadratics

Method 1 – Splitting the middle term

Method two – Fraction

Method 3 – Monic to non-monic

Method 4 – Cross Method

Method 5 – By Inspection

Method 6 – Grid

Infinite Product Expansion of cos (x)

Solving Cubic Functions

Recent Posts

Categories

Archives