Category Archives: Volume of Frustrum

December 14, 2024 · 6:56 am

Volume and Surface Area of a Conical Frustrum

My best attempt at drawing a Frustrum in Geogebra.

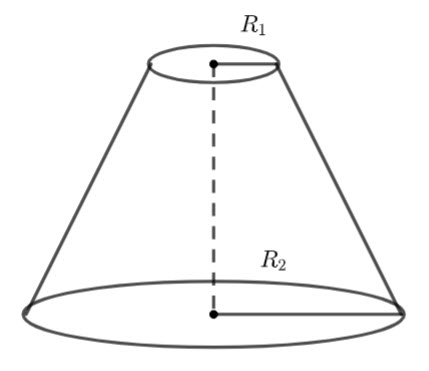
We have a truncated cone,

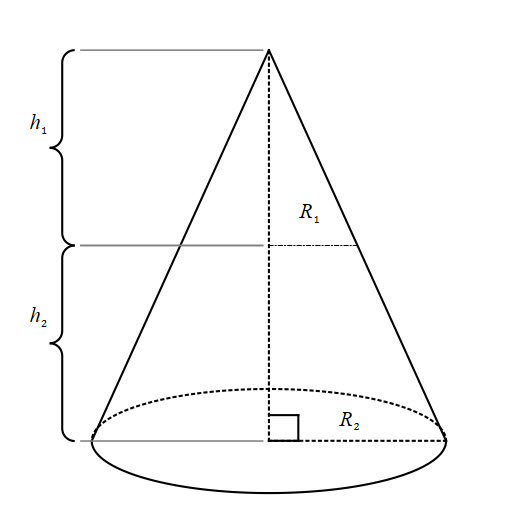
(1) $\begin{equation*}V=\frac{1}{3}\pi R_2^2(h_1+h_2)-\frac{1}{3}\pi R_1^2h_1\end{equation*}$

We are unlikely to know $h_1$ . Can we get $h_1$ in terms that we do know (i.e. $R_1, R_2, h_2$ )?

Think of similar triangles

Cross section of the cone

$\Delta ABC \sim \Delta ADE (AA)$

$R_1 \parallel R_2$

$\angle {C}=\angle{E}$ (Corresponding Angles in Parallel Lines)

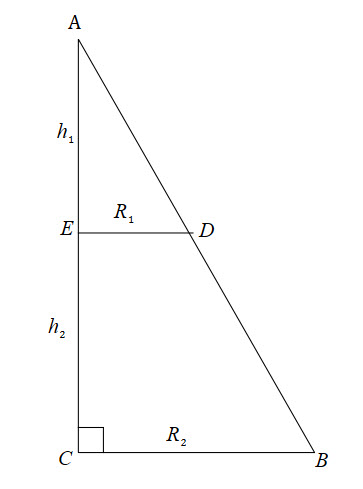
$\angle {B}=\angle {D}$ (Corresponding Angles in Parallel Lines)

Therefore

$\begin{equation*}\frac{h_1}{R_1}=\frac{h_1+h_2}{R_2}\end{equation}$

Rearrange to make $h_1$ the subject.

$\begin{equation*}h_1=\frac{h_2R_1}{R_2-R_1}\end{equation}$

Substitute into equation $(1)$

$\begin{equation*}V=\frac{1}{3} \pi((R_2^2(\frac{h_2R_1}{R_2-R_1})+h_2)-R_1^2(\frac{h_2R_1}{R_2-R_1}))\end{equation}$

$\begin{equation*}V=\frac{1}{3} \pi (R_2^2h_2+\frac{R_2^2h_2R_1}{R_2-R_1}-\frac{R_1^2h_2R_1}{R_2-R_1})\end{equation}$

$\begin{equation*}V=\frac{1}{3} \pi (R_2^2h_2+\frac{R_2^2h_2R_1-R_1^2h_2R_1}{R_2-R_1})\end{equation}$

$\begin{equation*}V=\frac{1}{3} \pi (R_2^2h_2+\frac{h_2R_1}{R_2-R_1}(R_2^2-R_1^2))\end{equation}$

$\begin{equation*}V=\frac{1}{3} \pi h_2(R_2^2+\frac{R_1}{R_2-R_1}(R_2-R_1)(R_2+R_1))\end{equation}$

$\begin{equation*}V=\frac{1}{3} \pi h_2(R_2^2+R_1(R_2+R_1))\end{equation}$

$\begin{equation*}V=\frac{1}{3} \pi h_2(R_2^2+R_1 R_2+R_1^2)\end{equation}$

Now let’s think about the surface area.

The surface area of a cone is $A=\pi r^2+\pi rs$ where $s$ is the slant height of the cone.

Once again, we need to subtract the ‘missing’ part of the cone.

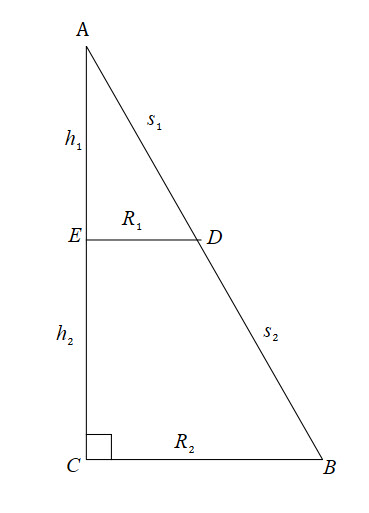
(2) $\begin{equation*}A=\pi R_2^2+\pi R_2(s_1+s_2)+ \pi R_1^2- \pi R_1s_1\end{equation*}$

We don’t need to subtract the circle of the top cone because it is the top of the frustrum, but we do need to add it on.

Using similar triangles again

$\begin{equation*}\frac{s_1}{R_1}=\frac{s_1+s_2}{R_2}\end{equation}$

$\begin{equation*}s_1=\frac{s_2R_1}{R_2-R_1}\end{equation}$

Substitute into equation $(2)$

$\begin{equation*}A=\pi(R_2^2+R_2(\frac{s_2R_1}{R_2-R_1}+s_2)+\pi R_1^2-R_1(\frac{s_2R_1}{R_2-R_1}))\end{equation}$

$\begin{equation*}A=\pi(R_2^2+R_2s_2+R_1^2+\frac{s_2R_1}{R_2-R_1}(R_2-R_1))\end{equation}$

$\begin{equation*}A=\pi(R_2^2+R_2s_2+R_1s_2+R_1^2)\end{equation}$

$\begin{equation*}A =\pi (R_1^2+s_2(R_1+R_2)+R_2^2)\end{equation}$

And hence the curved surface area is $\pi s_2(R_1+R_2)$ .

Leave a Comment

Filed under Area, Area of Frustrum, Interesting Mathematics, Measurement, Volume of Frustrum

Tagged as frustrum, surface area, volume