Category Archives: Geometry

January 2, 2026 · 7:08 am

Geometry Puzzle (finding a fraction of an area)

Geometry Puzzles in Felt Tip: A Compilation of puzzles from 2018 – Catriona Shearer

Band $1$ and $3$ have the same area.

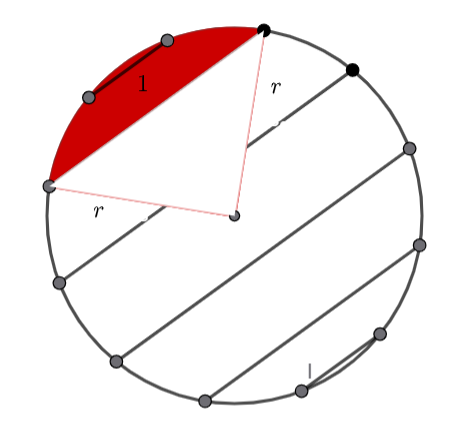
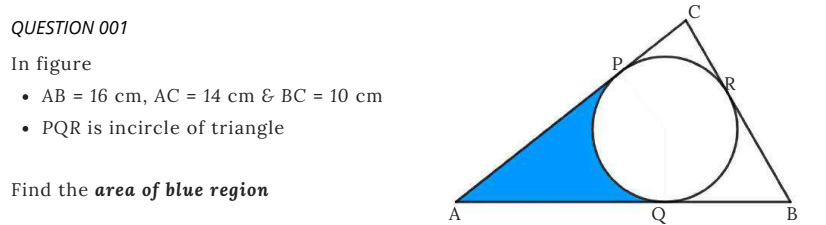
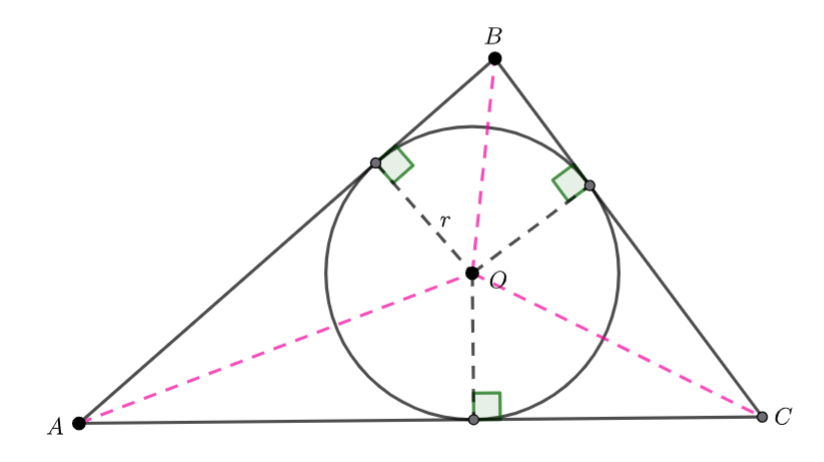
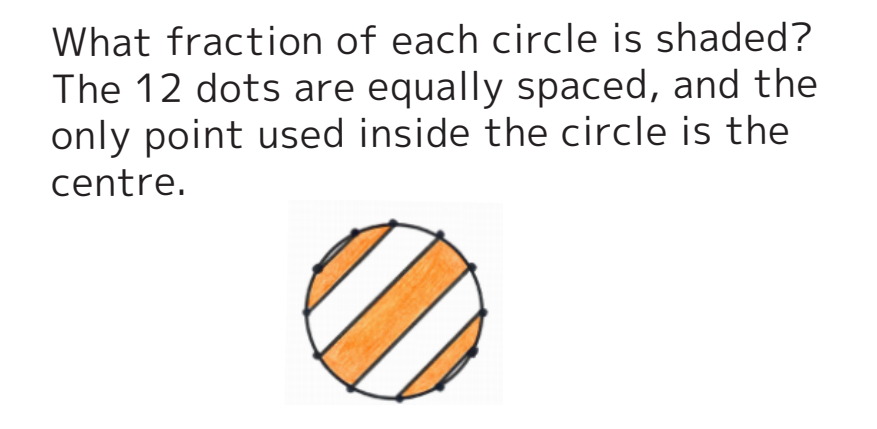
We want to find the area of the shaded segment.

As the dots are equally spaced, the sector’s angle is $\frac{\pi}{2} = (\frac{2\pi}{12}\times 3)$

Remember the area of a segment is $A=\frac{1}{2}r^2(\theta-sin(\theta))$ where the angle measurement is in radians.

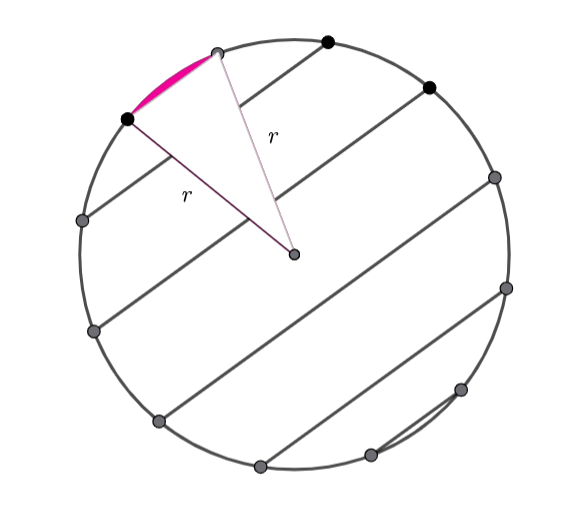
(1) $\begin{equation*}A=\frac{1}{2}r^2(\frac{\pi}{2}-sin(\frac{\pi}{2}))=\frac{1}{2}r^2(\frac{\pi}{2}-1))=\frac{\pi r^2}{4}-\frac{r^2}{2}\end{equation*}$

We want to find the area of the shaded segment.

As the dots are equally spaced, the sector’s angle is $\frac{2\pi}{12} = (\frac{\pi}{6})$

(2) $\begin{equation*}A=\frac{1}{2}r^2(\frac{\pi}{6}-sin(\frac{\pi}{6}))=\frac{\pi r^2}{12}-\frac{r^2}{4}\end{equation*}$

The area of band $1$ is equation $1 -$ equation $2$ .

(3) $\begin{equation*}\frac{\pi r^2}{4}-\frac{r^2}{2}-(\frac{\pi r^2}{12}-\frac{r^2}{4})=\frac{\pi r^2}{6}-\frac{r^2}{4}\end{equation*}$

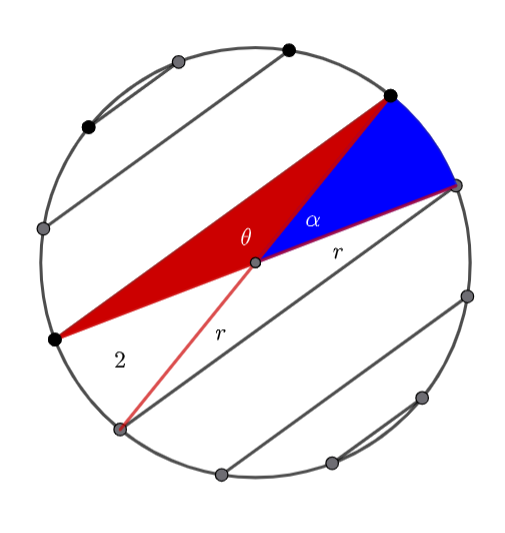
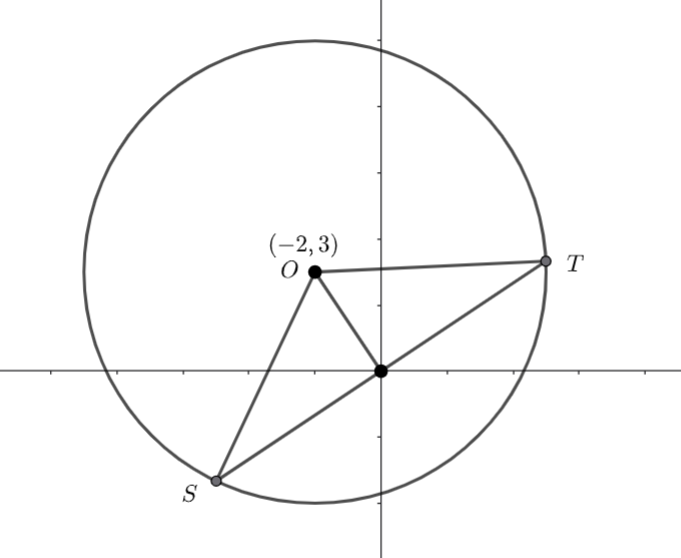
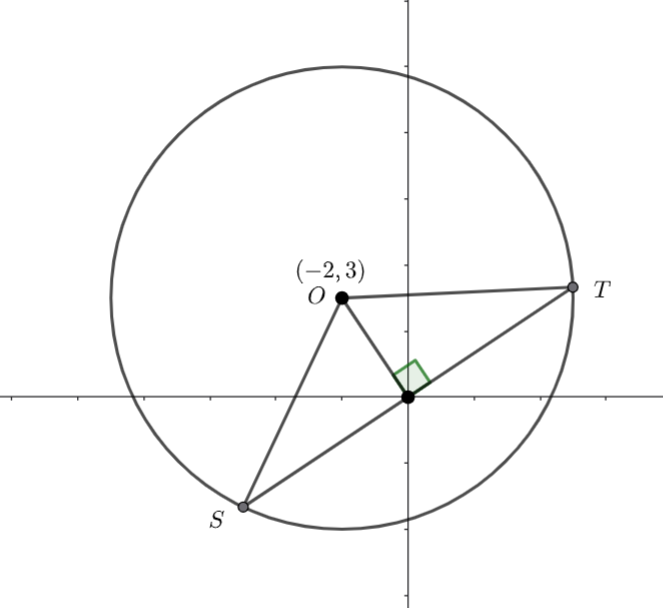
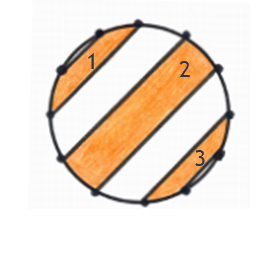
Band 2 consists of two congruent triangles and two congruent sectors.

$\begin{equation*}\theta=\frac{2\pi}{12}\times 5=\frac{5\pi}{6}, \alpha=\frac{\pi}{6}\end{equation}$

(4) $\begin{equation*}A=2(\frac{1}{2}r^2sin(\frac{5\pi}{6}))+2(\frac{1}{2}r^2\frac{\pi}{6})=\frac{r^2}{2}+\frac{r^2 \pi}{6}\end{equation*}$

Hence the shaded area is $2(\frac{\pi r^2}{6}-\frac{r^2}{4})+\frac{r^2}{2}+\frac{r^2 \pi}{6}=\frac{\pi r^2}{2}$

The area of the circle is $\pi r^2$

Hence the fraction of the shaded area is $=\frac{\frac{\pi r^2}{2}}{\pi r^2}=\frac{1}{2}$

Leave a Comment

Filed under Area, Area of Triangles (Sine), Finding an area, Geometry, Puzzles, Simplifying fractions

Tagged as catriona shearer, finding an area, geometry, geometry puzzle

December 10, 2025 · 7:54 am

Geometry Problem

Problem from *50 Maths Problems with Solutions* – Ajmal KP

The blue shaded area is the area of triangles $APO$ and $AQO$ subtract the sector $POQ$ .

We can use Heron’s law to find the area of the triangle $\Delta{ABC}$

$\begin{equation*}A=\sqrt{s(s-a)(s-b)(s-c)}\end{equation}$

where $s=\frac{a+b+c}{2}$

$\begin{equation*}A=\sqrt{20(20-16)(20-10)(20-14)}=40\sqrt{3}\end{equation}$

We also know the area of triangle $\Delta{ABC}=sr$ where $r$ is the radius of the inscribed circle.

Hence, $40\sqrt{3}=20r$ and $r=2\sqrt{3}$

We know $AP=AQ, CQ=CR$ , and $BP=BR$ – tangents to a circle are congruent.

$\begin{equation*}14-x=6+x\end{equation}$

(1) $\begin{equation*}8=2x\end{equation*}$

(2) $\begin{equation*}x=4\end{equation*}$

Area $\Delta{AQO}=\frac{1}{2}10\times 2\sqrt{3}=10\sqrt{3}$

Area $\Delta{APO}=$ Area $\Delta{AQO}$

$\begin{equation*}tan(\theta)=\frac{10}{2\sqrt{3}}\end{equation}$

$\begin{equation*}\theta=70.9^{\circ}\end{equation}$

Area of sector $OPQ=\frac{2\times70.9}{360}\pi (2\sqrt{3})^2=14.8$

Blue area = $20\sqrt{3}-14.8=19.8cm^2$

Leave a Comment

Filed under Algebra, Area, Finding an angle, Finding an area, Geometry, Heron's Law, Interesting Mathematics, Puzzles, Radius and Semi-Perimeter, Right Trigonometry, Solving Equations, Trigonometry

Tagged as geometry puzzle

December 4, 2025 · 12:52 pm

Area of a triangle from the semi-perimeter and the radius of the incircle.

$\begin{equation*}A=sr\end{equation}$

Where $s$ is the semi-perimeter, $s=\frac{a+b+c}{2}$ and $r$ is the radius of the incircle.

$AB, BC$ and $AC$ are tangents to the circle. And the radii are perpendicular to the tangents.

Add line segments $AO, CO$ and $BO$ .

$\Delta{ABC}$ is split into three triangles, $\Delta{AOB}, \Delta{AOC}$ and $\Delta{BOC}$ .

Hence Area $\Delta{ABC}=\Delta{AOB}+\Delta{AOC}+\Delta{BOC}$

$\Delta{ABC}=\frac{1}{2}cr+\frac{1}{2}br+\frac{1}{2}ar$

$\Delta{ABC}=\frac{1}{2}r(a+b+c)$

Remember $s=\frac{1}{2}(a+b+c)$

$\Delta{ABC}=sr$

1 Comment

Filed under Area, Finding an area, Geometry, Interesting Mathematics, Radius and Semi-Perimeter

November 16, 2025 · 5:54 am

Geometry Circle Question

In the diagram below, $A, B, C$ and $D$ lie on the circle with centre $O$ . If $\angle{DBC} = 41^{\circ}$ and $\angle{ACD} = 53^{\circ}$ , determine with reasoning $\angle{BAC}$ and $\angle{AOB}$

We know $OA=OB=OD$ – radii of the circle.

Which means, $\Delta{AOB}$ is isosceles and $\angle{OAB}=\angle{OBA}$ – equal angles isosceles triangle.

$\angle{AOD}=2\angle{ACD}$ – angle at the centre twice the angle at the circumference.

$\angle{AOB}=106^{\circ}$

This means $\angle{AOB}=74^{\circ}$ – angles on a straight line are supplementary

$\angle{OAD}=\angle{ODA}=37^{\circ}$ – equal angles isosceles triangle and the angle sum of a triangle.

$\angle{DBA}=\angle{DCA}=53^{\circ}$ – angle at the circumference subtended by the same arc are congruent.

$\angle{CAD}=\angle{CBD}=41^{\circ}$ – angles at the circumference subtended by the same arc are congruent.

$\angle{OAB}=53^{\circ}$ – equal angle isosceles triangle

Hence $\angle{BAC}=12^{\circ}$

Leave a Comment

Filed under Circle Theorems, Finding an angle, Geometry, Year 11 Specialist Mathematics

Tagged as circle theorems, geometry, Year 11 Specialist Mathematics

November 5, 2025 · 6:57 am

Equation of a Circle and Geometry Question

A circle has equation $x^2+y^2+4x-6y=36$
(a) Find the centre and radius of the circle.
Points $S$ and $T$ lie on the circle such that the origin is the midpoint of $ST$ .
(b) Show that $ST$ has a length of 12.

(a)We need to put the circle equation into completed square form

$\begin{equation*}(x+2)^2-4+(y-3)^2-9=36\end{equation}$

$\begin{equation*}(x+2)^2+(y-3)^2=49\end{equation}$

The centre is $(-2, 3)$ and the radius is $7$ .

(b)Draw a diagram

We know $SO$ and $TO$ are radii of the circle. Hence $\Delta{SOT}$ is isosceles and the line segment from $O$ to the origin is perpendicular to $ST$ .

$OT=7$ and the distance from $O$ to the origin is

$\begin{equation*}\sqrt{(-2-0)^2+(3-0)^2}=\sqrt{13}\end{equation}$

We can use Pythagoras to find the distance from the origin to $T$ .

$\begin{equation*}x=\sqrt{7^2-(\sqrt{13})^2}=\sqrt{49-13}=\sqrt{36}=6\end{equation}$

Hence $ST=2\times6=12$

Leave a Comment

Filed under Co-ordinate Geometry, Geometry, Pythagoras, Year 11 Mathematical Methods

September 30, 2025 · 3:54 am

Geometry Problem

*Geometry Snacks* by Ed Southall and Vincent Pantaloni

I started by trisecting another side of the triangle

This makes it clearer that the two lines are parallel

Which means the two angles labelled above are corresponding and therefore congruent.

Let the side length be $x$ .

The area of the equilateral triangle is

(1) $\begin{equation*}A=\frac{1}{2}x^2 sin(60)=\frac{\sqrt{3}x^2}{4}\end{equation*}$

$\begin{equation*}cos(60)=\frac{y}{\frac{2x}{3}}\end{equation}$

$\begin{equation*}y=\frac{x}{3}\end{equation}$

Area of right triangle

(2) $\begin{equation*}A=(\frac{1}{2})(\frac{2x}{3})(\frac{x}{3})sin(60)=\frac{\sqrt{3}x^2}{18}\end{equation*}$

The fraction of the area is

$\begin{equation*}=\frac{\frac{\sqrt{3}x^2}{18}}{\frac{\sqrt{3}x^2}{4}}=\frac{2}{9}\end{equation}$

Leave a Comment

Filed under Algebra, Area, Area of Triangles (Sine), Finding an area, Geometry, Puzzles, Right Trigonometry, Simplifying fractions, Trigonometry

Tagged as geometry problem, geometry snacks

September 9, 2025 · 11:19 am

Linear Transformation (Rotation) Question

The unit square is rotated about the origin by $45^\circ$ anti-clockwise.
(a) Find the matrix of this transformation.
(b) Draw the unit square and its image on the same set of axes.
(c) Find the area of the over lapping region.

Remember the general rotation matrix is

$\begin{equation*}\begin{bmatrix}cos(\theta)&-sin(\theta)\\sin(\theta)&cos(\theta)\end{bmatrix}\end{equation}$

Hence

$\begin{equation*}\begin{bmatrix}cos(45)&-sin(45)\\sin(45)&cos(45)\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}\end{equation}$

The unit square has co-ordinates

$\begin{bmatrix}0 & 1 & 1& 0\\0&0&1&1\end{bmatrix}$

Transform the unit square

$\begin{bmatrix}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}\begin{bmatrix}0 & 1 & 1& 0\\0&0&1&1\end{bmatrix}=\begin{bmatrix}0&\frac{1}{\sqrt{2}}&0&-\frac{1}{\sqrt{2}}\\0&\frac{1}{\sqrt{2}}&\frac{2}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}$

The overlapping area is the area of $\Delta ADC$ – the area of $\Delta EFC$

We know $\angle{FCE}=45^\circ$ because the diagonal of a square bisects the angle.

We know $\angle{EFC}$ is a right angle as it’s on a straight line with the vertex of a square.

Hence $\Delta EFC$ is isosceles.

$\overline{AC}=\sqrt{1^2+1^2}=\sqrt{2}$ and $\overline{AF}=1$ , hence $\overline{FC}=\sqrt{2}-1$

$A_{\Delta ADC}=\frac{1}{2}(1)(1)=\frac{1}{2}$

$A_{\Delta ECF}=\frac{1}{2}(\sqrt{2}-1)(\sqrt{2}-1)$

Area of shaded region = $\frac{1}{2}-\frac{1}{2}(3-2\sqrt{2})=\sqrt{2}-1$

Leave a Comment

Filed under Area, Co-ordinate Geometry, Finding an area, Geometry, Matrices, Transformations, Year 11 Specialist Mathematics

Tagged as matrix tranformations, rotations

September 6, 2025 · 9:50 am

Clock (Geometry Question)

At what time after 2pm will the minute hand over take the hour hand?

Let the distance the minute hand moves be $x^\circ$ . Then the distance the hour hand moves is $x-60^\circ$ (The angle between the hands at 2pm is $60^\circ$ )

The rate the hour hand moves is $R_H=\frac{30}{60}=\frac{1}{2}^\circ$ per minute, and the rate the minute hand moves is $R_M=\frac{360}{60}=6^\circ$ per minute.

The time is the distance divided by the rate,

$\begin{equation*}\frac{x}{6}=\frac{x-60}{\frac{1}{2}}\end{equation}$

$\begin{equation*}\frac{x}{2}=6x-360\end{equation}$

$\begin{equation*}360=\frac{11x}{2}\end{equation}$

$\begin{equation*}x=65\frac{5}{11}^\circ\end{equation}$

As the minute hand moves $65\frac{5}{11}^\circ$ , the change in time is $65\frac{5}{11}^\circ \div 6=10$ minutes and $54$ seconds. Hence the time is $2:11$ pm

Leave a Comment

Filed under Finding an angle, Geometry, Puzzles

Tagged as geometry clock question

May 24, 2025 · 10:02 am

Circle Geometry Problem

In the diagram, points $A, B, C, D$ and $Q$ lie on a circle centre $O$ , radius $6$ cm and diameter $BQ, \angle{ABQ}=50^\circ, AB$ is parallel to $DO$ and point $P$ lies on diameter $BQ$ such that $OP=DP=4$ cm.

(a) Find $\angle{BCD}$

(b) Determine the length of $PC$ .

$\angle{BOD}=180^\circ-50^\circ=130^\circ$ (Co-interior angles in parallel lines are supplementary.)

$\angle{BCD}=\frac{1}{2}\times 130=65^\circ$ (Angles subtended by the same arc. The angle at the centre is twice the angle at the circumference.)

$\angle{BCD}=65^\circ.$

Let $PC=x$

From the intersecting chord theorem

$\begin{equation*}4\times x=2\times 10\end{equation}$

$\begin{equation*}4x=20\end{equation}$

$\begin{equation*}x=5\end{equation}$

$PC=5cm$

A chord $AB$ of a circle $O$ is extended to $C$ . The straight line bisecting $\angle{OAB}$ meets the circle at $E$ . Let $\angle{BAE}=x$ . Prove that $EB$ bisects $\angle{OBC}$ .

$\angle{BAO}=2x$ ( $AE$ bisects $\angle {BAO}$ )

$\Delta AOB$ is isosceles ( $AO=B0$ radii of the circle)

$\angle{ABO}=2x$ (Equal angles in isosceles triangle)

Therefore $\angle {AOB}=180^\circ-4x$ (angle sum of a triangle)

$\angle {BEA}=90^\circ-2x$ (angle at the circumference is half angle at the centre)

$\angle{ABE}=180^\circ-x-(90^\circ-2x)=90^\circ+x$ (angle sum of a triangle)

$\angle{CBE}=180^\circ-(90^\circ+x)=90^\circ-x$ (angles on a straight line)

$\angle{OBE}=90^\circ+x-2x=90^\circ-x$

$\angle{OBE}=\angle{CBE}$

Hence, $BE$ bisects $\angle{OBC}$

Leave a Comment

Filed under Circle Theorems, Geometry, Uncategorized, Year 11 Specialist Mathematics

Tagged as circle geometry, circle theorems

May 3, 2025 · 3:34 am

Geometry Puzzle

Another puzzle from this book

Two ladders are propped up vertically in a narrow passageway between two vertical buildings. The ends of the ladders are 8 metres and 4 metres above the pavement.
Find the height above the ground, $T$ ,