Category Archives: Chain Rule

October 20, 2025 · 11:11 am

Fundamental Theorem of Calculus

(1)   \begin{equation*}\frac{d}{dx} \left (\int_2^{f(x)} g(t) dt \right )=g(f(x))f'(x)\end{equation*}

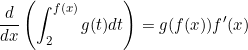
My Year 12 Mathematics Methods students are getting ready for their exam, and questions using the above idea have created a bit of consternation. I am going to work through an example, and show why the ‘formula’ works.

Example

Find \frac{d}{dx} \left ( \int_2^{x^2} 4t^2+3t \enspace dt \right ).

    \begin{equation*}=\frac{d}{dx} \left (\frac{4t^3}{3}+\frac{3t^2}{2} \right ]_2^{x^2}\end{equation}

    \begin{equation*}=\frac{d}{dx} \left ( \frac{4(x^2)^3}{3}+\frac{3(x^2)^2}{2} -(\frac{4(2^3)}{3}+\frac{3(2^2)}{2} \right )\end{equation}

    \begin{equation*}=\frac{d}{dx} \left (\frac{4x^6}{3}+\frac{3x^4}{2}-\frac{50}{3} \right) \end{equation}

    \begin{equation*}=\frac{24x^5}{3}+\frac{12x^3}{2}\end{equation}

(2)   \begin{equation*}=8x^5+6x^3\end{equation*}

If we used ‘formula’ 1

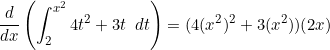
    \begin{equation*}\frac{d}{dx} \left ( \int_2^{x^2} 4t^2+3t \enspace dt \right )=(4(x^2)^2+3(x^2))(2x)\end{equation}

\

(3)   \begin{equation*}\frac{d}{dx} \left ( \int_2^{x^2} 4t^2+3t \enspace dt \right )=8x^5+6x^3 \end{equation*}

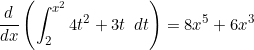
We can see equation 2 and 3 are the same.

More formally

    \begin{equation*}\frac{d}{dx} \left ( \int_c^{f(x)} g(t) dt \right )=\frac{d}{dx} \left (G(f(x))-G(c) \right ) \end{equation}

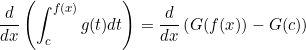
Remember \frac{d}{dx} \left (f(g(x)) \right )=f'(g(x))\times g'(x)

    \begin{equation*}\frac{d}{dx} \left (G(f(x))-G(c) \right ) =G'(f(x))f'(x)=g(f(x))\times f'(x)\end{equation}

Leave a Comment

Filed under Calculus, Chain Rule, Differentiation, Integration, Year 12 Mathematical Methods

Tagged as ,

January 9, 2025 · 9:40 am

Deriving the Chain Rule for Differentiation

How to differentiate something in the form y=[f(x)]^n

For example, y=(3x^2-2x+6)^5, we could expand the expression, but the Chain Rule provides a quick and easy method.

Differentiate y=[f(x)]^n

Let u=f(x), then y=u^n

We want to find \frac{dy}{dx}, but \frac{dy}{dx}=\frac{dy}{du}\times \frac{du}{dx}

They’re not fractions, but limits of fractions, but they work like fractions.

\frac{du}{dx}=f'(x) and \frac{dy}{du}=nu^{n-1}

Therefore, \frac{dy}{dx}=f'(x)\times nu^{n-1}

Replace u with f(x)

(1)   \begin{equation*}\frac{dy}{dx}=n[f(x)]^{n-1}f'(x)\end{equation*}

What about a function in the form y=f(g(x))?

We’re going to follow the same process.

Let u=g(x), then y=f(u)

\frac{du}{dx}=g'(x) and \frac{dy}{du}=f'(u)

Therefore \frac{dy}{dx}=f'(u)g'(x)

(2)   \begin{equation*}\frac{dy}{dx}=f'(g(x))g'(x) \end{equation*}

Equations 1 and 2 are versions of the Chain Rule.

Example

Find the derivative of y=(3x^2-2x+6)^5

    \begin{equation*}\frac{dy}{dx}=5(3x^2-2x+6)^4\times (6x-2)\end{equation}

    \begin{equation*}\frac{dy}{dx}=5(6x-2)(3x^2-2x+6)^4\end{equation}

    \begin{equation*}\frac{dy}{dx}=10(3x-1)(3x^2-2x+6)\end{equation}

Next time we are going to look at the Product Rule.

1 Comment

Filed under Calculus, Chain Rule, Differentiation, Year 12 Mathematical Methods

Tagged as , , ,