Category Archives: Simplifying fractions

I use synthetic division to factorise polynomials with a degree greater than 2. For example,

It works best with monic polynomials but can be adapted to non-monic ones (see example below).

The only problem is that you need to find a root to start.

Try the factors of i.e.

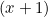Hence, is a root and is a factor of the polynomial.

Set up as follows

Bring the first number down

Multiply by the root and place under the second co-efficient

Add down

Repeat the process

The numbers at the bottom are the coefficients of the polynomial factor.

We now know .

We can factorise the quadratic in the usual way.

Hence .

Let’s try a non-monic example

Factorise

I know is a root. Otherwise I would try the factors of 30.

Use synthetic division

Because this was non-monic we need to divide our new co-efficients by 6 (the co-efficient of the term)

We now need to go again. I know that is a root and is a factor.

Our quadratic factor is , which is .

The quadratic factor doesn’t have integer factors so,

I think this is much quicker than polynomial long division.