I was working on a question and involved 11 and I wondered what the divisibility rule was?
So then I had a bit of a think about it.
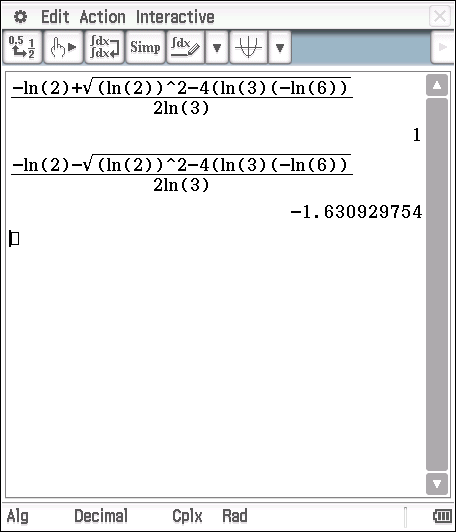
Let ![]() be a number divisible by
be a number divisible by ![]() . The
. The ![]()
![]()
![]()
Now ![]() which is congruent to
which is congruent to ![]() because
because ![]() , which is a multiple of 11.
, which is a multiple of 11.
Thus
![]()
Odd powers will be negative and even positive.
So if we start at one end of the number and add every second digit (i.e. first digit plus third digit plus fifth digit etc.) and then subtract the other digits (i.e. second digit, fourth digit, six digit, etc.), if that equals zero then the number is divisible by 11.
For example, is ![]() divisible by
divisible by ![]() ?
?
![]()
Hence ![]() is divisible by
is divisible by ![]()