March 5, 2025 · 2:00 am
↓ Jump to Comments

Binomial Expansion Theorem

My Year 11 Mathematics Methods students are working on the Binomial Expansion Theorem.

But before we get onto that, remember Pascal’s triangle

First 8 rows of Pascal’s triangle

Now we can use combinations to find the numbers in each row. For example, 1 4 6 4 1 is \begin{pmatrix}4\\0\end{pmatrix}=1, \begin{pmatrix}4\\1\end{pmatrix}=4, \begin{pmatrix}4\\2\end{pmatrix}=6, \begin{pmatrix}4\\3\end{pmatrix}=4, \begin{pmatrix}4\\4\end{pmatrix}=1

ExpressionExpansionCo-efficients
(x+y)^2x^2+2xy+y^21, 2, 1
(x+y)^3x^3+3x^2y+3xy^2+y^31, 3, 3, 1
(x+y)^4x^4+4x^3y+6x^2y^2+4xy^3+y^41, 4, 6, 4, 1

As you can see, the coefficients are the row of pascal’s triangle corresponding to the power. So (x+y)^6 would have co-efficients from the sixth row of the table 1, 6, 15, 20, 15, 6, 1.

To generalise

(x+y)^n=\begin{pmatrix}n\\0\end{pmatrix}x^ny^0+\begin{pmatrix}n\\1\end{pmatrix}x^{n-1}y^1+\begin{pmatrix}n\\2\end{pmatrix}x^{n-2}y^2+ ...+\begin{pmatrix}n\\n-1\end{pmatrix}x^1{y^{n-1}+\begin{pmatrix}n\\n\end{pmatrix}x^0y^n

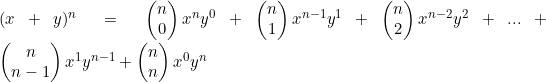
Which we can condense to

(x+y)^n=\Sigma_{i=0}^n \begin{pmatrix}n\\i\end{pmatrix}x^{n-i}y^i

Worked Examples

(1) Expand (2x-3)^4

(2x-3)^4=\begin{pmatrix}4\\0\end{pmatrix}(2x)^4(-3)^0+\begin{pmatrix}4\\1\end{pmatrix}(2x)^3(-3)^1+\begin{pmatrix}4\\2\end{pmatrix}(2x)^2(-3)^2+\begin{pmatrix}4\\3\end{pmatrix}(2x)^1(-3)^3+\begin{pmatrix}4\\4\end{pmatrix}(2x)^0(-3)^4
(2x-3)^4=16x^4-96x^3+216x^2-216x+81

(2) Find the co-efficient of the x^3 term in the expansion of (2-5x)^5.

Remember (x+y)^n=\Sigma_{i=0}^n \begin{pmatrix}n\\i\end{pmatrix}x^{n-i}y^i, the x^3 is when i=3
\begin{pmatrix}5\\3\end{pmatrix}(2)^2(-5)^3=10\times 2\times -125=-5000

(3) Find the constant term in the expansion of (x^2+\frac{3}{x^4})^6

We need to find the term where the x‘s cancel out. Each term is \begin{pmatrix}6\\i\end{pmatrix}(x^2)^{6-i}(\frac{3}{x^4})^i.
\begin{pmatrix}6\\i\end{pmatrix}(x^{12-2i})(3^ix^{-4i}).
We need 12-2i-4i=0, hence i=2
Therefore, the co-efficient is \begin{pmatrix}6\\2\end{pmatrix}\times3^2=135

1 Comment

Filed under Algebra, Binomial Expansion Theorem, Counting Techniques, Year 11 Mathematical Methods

One Response to Binomial Expansion Theorem

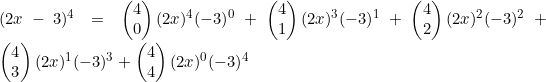
  1. Pingback: Continuous Uniform Random Variable | Racquel Sanderson

Leave a Reply

Your email address will not be published. Required fields are marked *