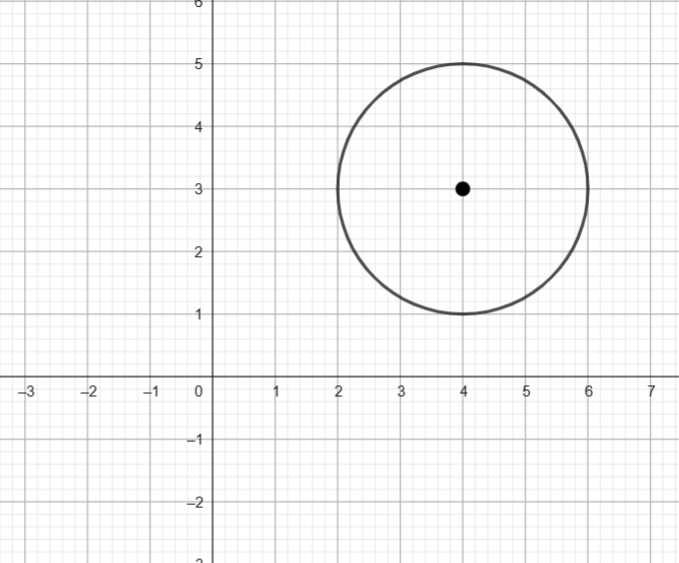
A sketch of the locus of a complex number 
is shown above, determine the maximum value of 
correct to two decimal places where 
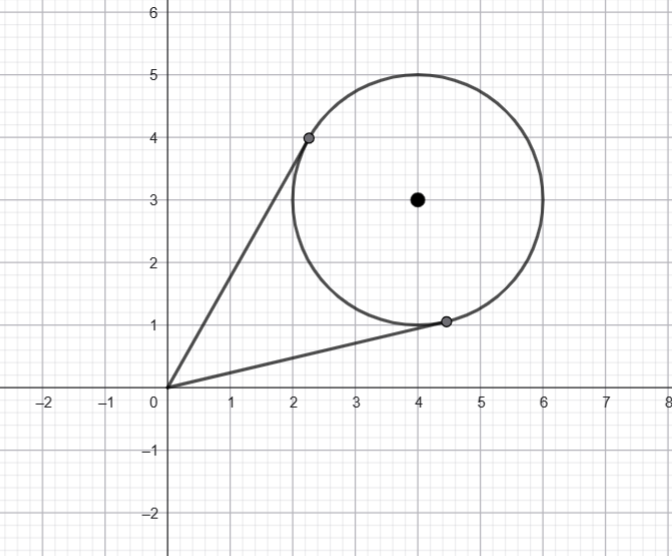
Draw tangent lines from the origin to the circle.
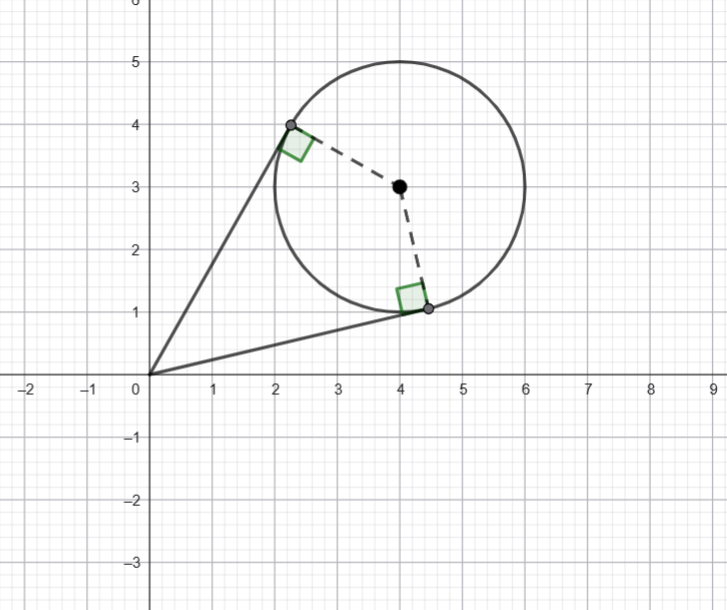
Remember tangent lines are perpendicular to the radii
The maximum argument is this angle
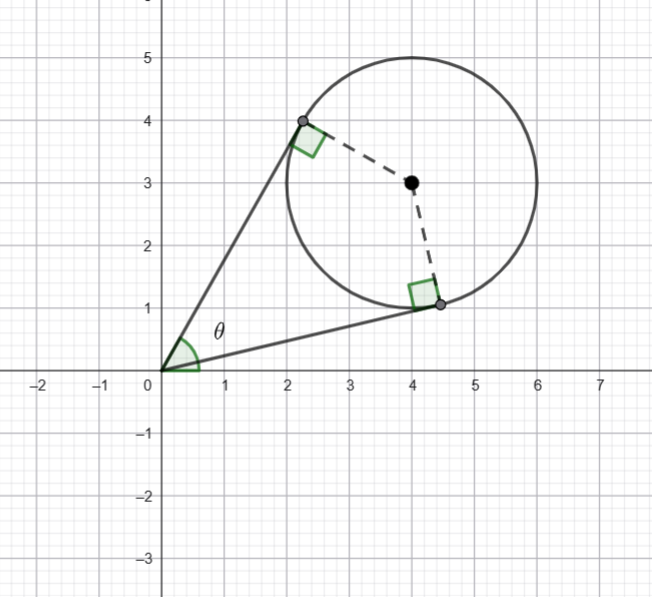
I am going to find the angle in two sections
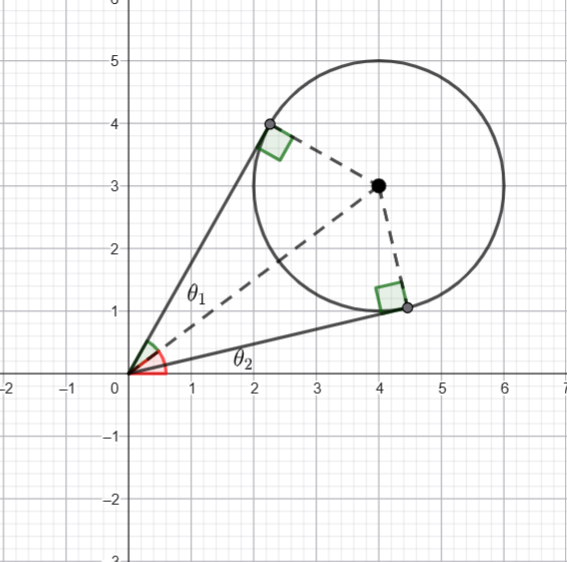
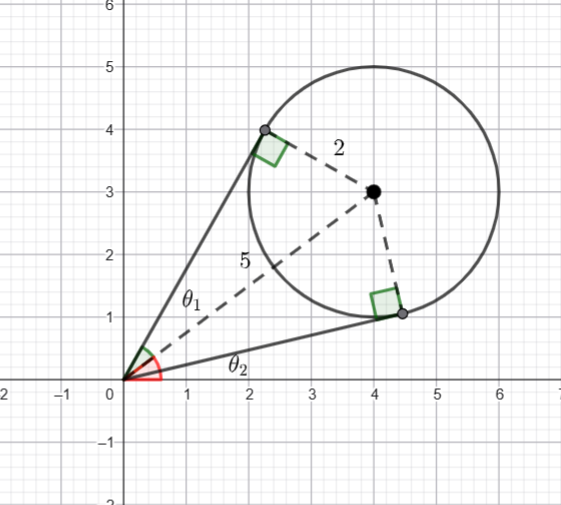
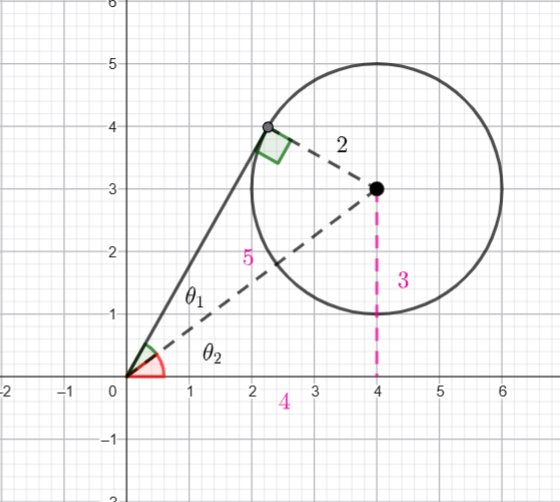
From the diagram the radius of the circle is 
and the centre is 
. Hence the distance from the origin to the centre is 
.
Hence maximum 