
![]()
Where ![]() is the semi-perimeter,
is the semi-perimeter, ![]() and
and ![]() is the radius of the incircle.
is the radius of the incircle.
![]() and
and ![]() are tangents to the circle. And the radii are perpendicular to the tangents.
are tangents to the circle. And the radii are perpendicular to the tangents.
Add line segments ![]() and
and ![]() .
.
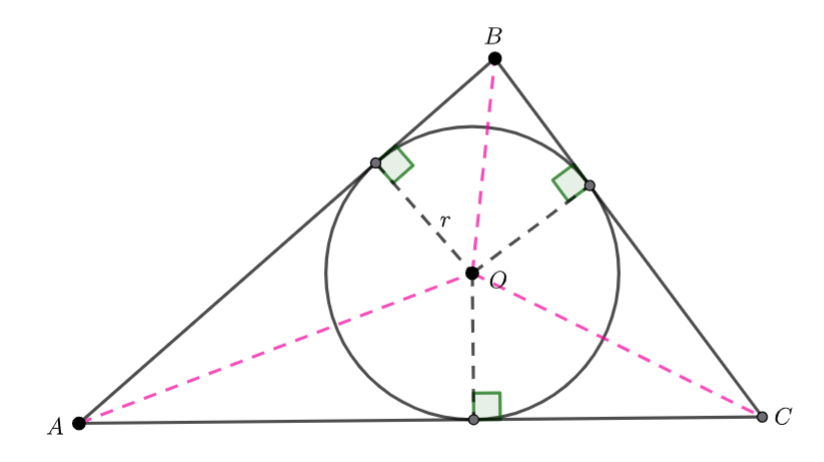
![]() is split into three triangles,
is split into three triangles, ![]() and
and ![]() .
.
Hence Area ![]()
![]()
![]()
Remember ![]()
![]()

![]()
Where ![]() is the semi-perimeter,
is the semi-perimeter, ![]() and
and ![]() is the radius of the incircle.
is the radius of the incircle.
![]() and
and ![]() are tangents to the circle. And the radii are perpendicular to the tangents.
are tangents to the circle. And the radii are perpendicular to the tangents.
Add line segments ![]() and
and ![]() .
.

![]() is split into three triangles,
is split into three triangles, ![]() and
and ![]() .
.
Hence Area ![]()
![]()
![]()
Remember ![]()
![]()
Filed under Area, Finding an area, Geometry, Interesting Mathematics, Radius and Semi-Perimeter
Pingback: Geometry Problem | Racquel Sanderson