I found a co-ordinate puzzle here.
Finished image
Filed under Co-ordinate Geometry
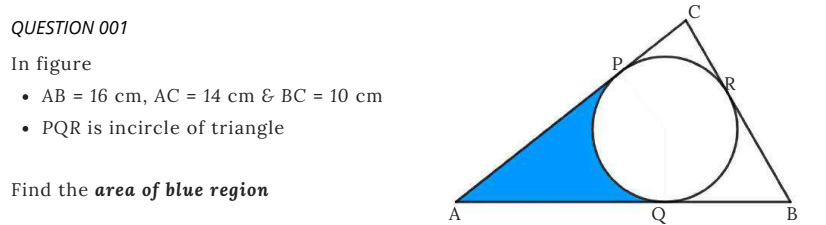
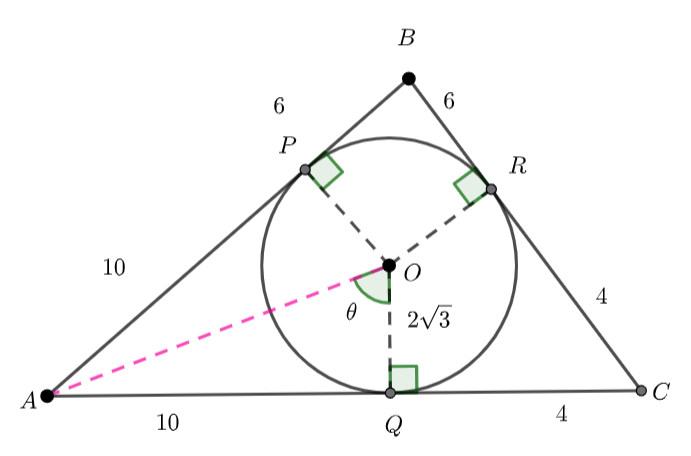
The blue shaded area is the area of triangles ![]() and
and ![]() subtract the sector
subtract the sector ![]() .
.
We can use Heron’s law to find the area of the triangle ![]()
![]()
where ![]()
![]()
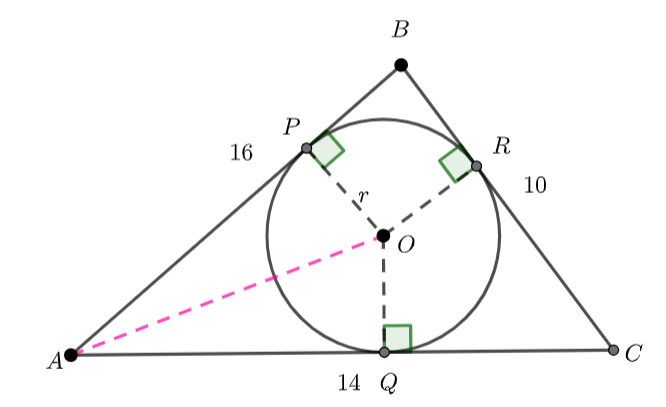
We also know the area of triangle ![]() where
where ![]() is the radius of the inscribed circle.
is the radius of the inscribed circle.
Hence, ![]() and
and ![]()
We know ![]() , and
, and ![]() – tangents to a circle are congruent.
– tangents to a circle are congruent.
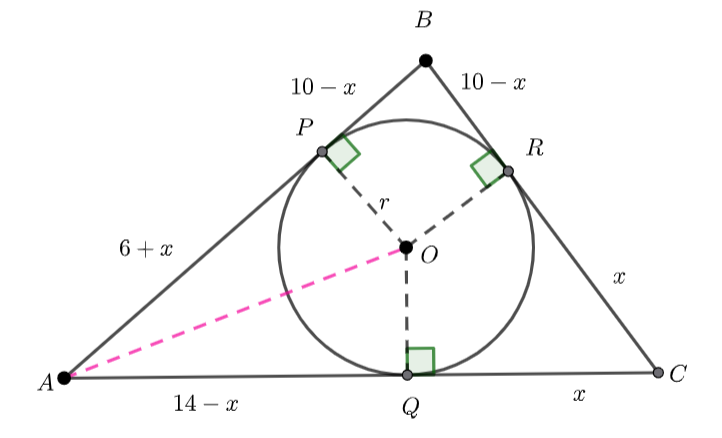
![]()
(1) ![]()
(2) ![]()
Area ![]()
Area ![]() Area
Area ![]()
![]()
![]()
Area of sector ![]()
Blue area = ![]()

![]()
Where ![]() is the semi-perimeter,
is the semi-perimeter, ![]() and
and ![]() is the radius of the incircle.
is the radius of the incircle.
![]() and
and ![]() are tangents to the circle. And the radii are perpendicular to the tangents.
are tangents to the circle. And the radii are perpendicular to the tangents.
Add line segments ![]() and
and ![]() .
.
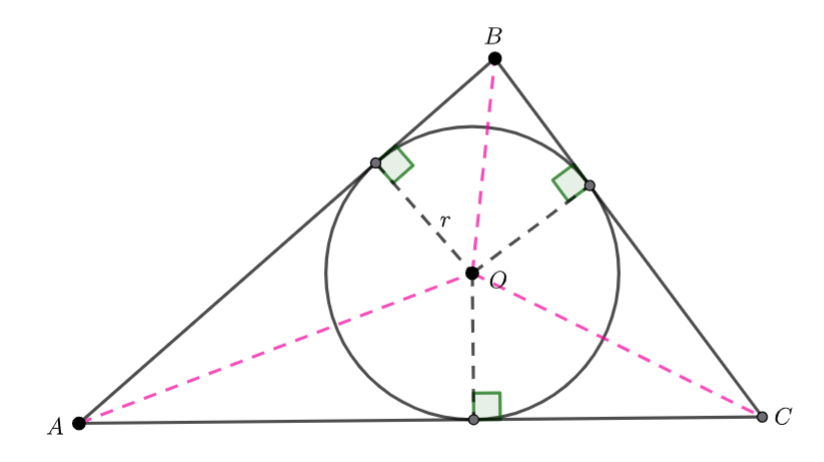
![]() is split into three triangles,
is split into three triangles, ![]() and
and ![]() .
.
Hence Area ![]()
![]()
![]()
Remember ![]()
![]()
Filed under Area, Finding an area, Geometry, Interesting Mathematics, Radius and Semi-Perimeter