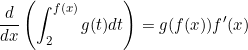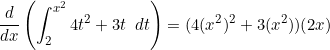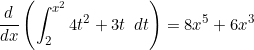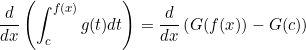Monthly Archives: October 2025

October 28, 2025 · 5:42 am

Integration Question (much easier with Integration by Parts)

The Year 12 Mathematics Methods course doesn’t cover Integration by Parts, so they end up with questions like the following.

Determine the following:
(a) $\frac{d}{dx} \left (e^{2x}sin(3x) \right )$
(b) $\frac{d}{dx} \left (e^{2x}cos(3x) \right )$
Hence, determine the following integral by considering both parts (a) and (b)
$\int_0^{\frac{\pi}{2}}13e^{2x}cos(3x) \enspace dx$

(a) Use the product rule

(1) $\begin{equation*}\frac{d}{dx} \left (e^{2x}sin(3x) \right)= 2e^{2x}sin(3x)+3e^{2x}cos(3x) \end{equation*}$

(b)

(2) $\begin{equation*}\frac{d}{dx} \left (e^{2x}cos(3x) \right )=2e^{2x}cos(3x)-3e^{2x}sin(3x)\end{equation*}$

I need to use equations $1$ and $2$ to find $\int_0^{\frac{\pi}{2}}13e^2xcos(3x) \enspace dx$ .

The $e^{2x}sin(3x)$ terms need to vanish and I need $13$ of the $e^{2x}cos(3x)$ terms.

$3\times \text{equation} (1)+ 2\times \text{equation} (2)$

(3) $\begin{equation*}3\frac{d}{dx} \left (e^{2x}sin(3x) \right)= 6e^{2x}sin(3x)+9e^{2x}cos(3x) \end{equation*}$

(4) $\begin{equation*}2\frac{d}{dx} \left (e^{2x}cos(3x) \right )=4e^{2x}cos(3x)-6e^{2x}sin(3x)\end{equation*}$

Equation $3$ plus equation $4$

(5) $\begin{equation*}3\frac{d}{dx} \left (e^{2x}sin(3x) \right)+2\frac{d}{dx} \left (e^{2x}cos(3x) \right )=13e^{2x}cos(3x)\end{equation*}$

Integrate both sides of the equation

$\int_0^{\frac{\pi}{2}} \left (3\frac{d}{dx} \left (e^{2x}sin(3x) \right)+2\frac{d}{dx} \left (e^{2x}cos(3x) \right ) \right ) dx=\int_0^{\frac{\pi}{2}}13e^{2x}cos(3x) \enspace dx$

By the fundamental theorem of calculus, we know

$(3e^{2x}sin(3x) \right)+2 \left (e^{2x}cos(3x) \right ]_0^{\frac{\pi}{2}}=\int_0^{\frac{\pi}{2}}13e^{2x}cos(3x) \enspace dx$

$3e^{\pi}sin(\frac{3\pi}{2}})+2e^{\pi}cos(\frac{3\pi}{2}})-3e^0sin(3(0))-2e^0cos(3(0))=\int_0^{\frac{\pi}{2}}13e^{2x}cos(3x) \enspace dx$

$\int_0^{\frac{\pi}{2}}13e^{2x}cos(3x) \enspace dx=-3e^{\pi}-2$

Integration by Parts

Remember $\int u\enspace dv=uv-\int v \enspace du$

$\int_0^{\frac{\pi}{2}}e^{2x}cos(3x) \enspace dx$

Let $u=cos(3x)$ , then $du=-3sin(3x)$

and $dv=e^{2x}$ , then $v=\frac{e^{2x}}{2}$

$\int_0^{\frac{\pi}{2}}e^{2x}cos(3x) \enspace dx = \left (cos(3x)\left (\frac{e^{2x}}{2}\right ) \right )_0^{\frac{\pi}{2}}-\int_0^{\frac{\pi}{2}} \frac{e^{2x}}{2}(-3sin(3x)) \enspace dx$

$\int_0^{\frac{\pi}{2}}e^{2x}cos(3x) \enspace dx=cos(\frac{3\pi}{2})(\frac{e^\pi}{2})-cos(0)(\frac{e^0}{2})+\frac{3}{2}\int_0^{\frac{\pi}{2}}sin(3x)e^{2x} \enspace dx$

$\int_0^{\frac{\pi}{2}}e^{2x}cos(3x) \enspace dx=-\frac{1}{2}+\frac{3}{2}\int_0^{\frac{\pi}{2}}sin(3x)e^{2x} \enspace dx$

Let $u=sin(3x)$ , then $du=3cos(3x)$

and $dv=e^{2x}$ . then $v=\frac{e^{2x}}{2}$

$\int_0^{\frac{\pi}{2}}e^{2x}cos(3x) \enspace dx=-\frac{1}{2}+\frac{3}{2}(\frac{e^{2x}}{2}sin(3x)]_0^{\frac{\pi}{2}}-\int_0^{\frac{\pi}{2}} \frac{e^{2x}}{2}(3cos(3x)) \enspace dx)$

$\int_0^{\frac{\pi}{2}}e^{2x}cos(3x) \enspace dx=-\frac{1}{2}+\frac{3}{2}(-\frac{e^\pi}{2}-\frac{3}{2} \int_0^{\frac{\pi}{2}} e^{2x}cos(3x) \enspace dx)$

$\int_0^{\frac{\pi}{2}}e^{2x}cos(3x) \enspace dx=-\frac{1}{2}-\frac{3e^\pi}{4}-\frac{9}{4} \int_0^{\frac{\pi}{2}} e^{2x}cos(3x) \enspace dx$

Collect like terms (the integrals are like)

$\frac{13}{4}(\int_0^{\frac{\pi}{2}}e^{2x}cos(3x) \enspace dx)=-\frac{1}{2}-\frac{3e^\pi}{4}$

$(\int_0^{\frac{\pi}{2}}e^{2x}cos(3x) \enspace dx)=\frac{-2-3e^\pi}{13}$

Leave a Comment

Filed under Algebra, Calculus, Integration, Integration by Parts, Year 12 Mathematical Methods

Tagged as integration by parts

October 20, 2025 · 11:11 am

Fundamental Theorem of Calculus

(1) $\begin{equation*}\frac{d}{dx} \left (\int_2^{f(x)} g(t) dt \right )=g(f(x))f'(x)\end{equation*}$

My Year 12 Mathematics Methods students are getting ready for their exam, and questions using the above idea have created a bit of consternation. I am going to work through an example, and show why the ‘formula’ works.

Example

Find $\frac{d}{dx} \left ( \int_2^{x^2} 4t^2+3t \enspace dt \right )$ .

$\begin{equation*}=\frac{d}{dx} \left (\frac{4t^3}{3}+\frac{3t^2}{2} \right ]_2^{x^2}\end{equation}$

$\begin{equation*}=\frac{d}{dx} \left ( \frac{4(x^2)^3}{3}+\frac{3(x^2)^2}{2} -(\frac{4(2^3)}{3}+\frac{3(2^2)}{2} \right )\end{equation}$

$\begin{equation*}=\frac{d}{dx} \left (\frac{4x^6}{3}+\frac{3x^4}{2}-\frac{50}{3} \right) \end{equation}$

$\begin{equation*}=\frac{24x^5}{3}+\frac{12x^3}{2}\end{equation}$

(2) $\begin{equation*}=8x^5+6x^3\end{equation*}$

If we used ‘formula’ $1$

$\begin{equation*}\frac{d}{dx} \left ( \int_2^{x^2} 4t^2+3t \enspace dt \right )=(4(x^2)^2+3(x^2))(2x)\end{equation}$

(3) $\begin{equation*}\frac{d}{dx} \left ( \int_2^{x^2} 4t^2+3t \enspace dt \right )=8x^5+6x^3 \end{equation*}$

We can see equation $2$ and $3$ are the same.

More formally

$\begin{equation*}\frac{d}{dx} \left ( \int_c^{f(x)} g(t) dt \right )=\frac{d}{dx} \left (G(f(x))-G(c) \right ) \end{equation}$

Remember $\frac{d}{dx} \left (f(g(x)) \right )=f'(g(x))\times g'(x)$

$\begin{equation*}\frac{d}{dx} \left (G(f(x))-G(c) \right ) =G'(f(x))f'(x)=g(f(x))\times f'(x)\end{equation}$

Leave a Comment

Filed under Calculus, Chain Rule, Differentiation, Integration, Year 12 Mathematical Methods

Tagged as differentiation, fundamental theorem of calculus

October 15, 2025 · 6:19 am

Hard Equation Solving Question

Find the value(s) of $k$ such that the equation below has two numerically equal but opposite sign solutions (e.g. $5$ and $-5$ ).

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{k-1}{k+1}\end{equation}$

$\begin{equation*}(x^2-2x)(k+1)=(k-1)(4x-1)\end{equation}$

$\begin{equation*}(k+1)x^2-2kx-2x=4kx-k-4x+1\end{equation}$

$\begin{equation*}(k+1)x^2-2kx-4kx-2x+4x-1=0\end{equation}$

$\begin{equation*}(k+1)^2x^2-(6k-2)x-1=0\end{equation}$

For there to be two numerically equal but opposite sign solutions, the $b$ term of the quadratic equation must be $0$ .

$\begin{equation*}6k-2=0\end{equation}$

Hence $k=\frac{1}{3}$ .

When $k=\frac{1}{3}$ the equation becomes

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{\frac{-2}{3}}{\frac{4}{3}}\end{equation}$

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{-1}{2}\end{equation}$

$\begin{equation*}2x^2-4x=-4x+1\end{equation}$

$\begin{equation*}2x^2-1=0\end{equation}$

$\begin{equation*}x^2=\frac{1}{2}\end{equation}$

$\begin{equation*}x=\pm \frac{1}{\sqrt{2}}\end{equation}$

Leave a Comment

Filed under Algebra, Polynomials, Quadratic, Quadratics, Solving, Solving, Solving Equations

Tagged as hard algebra question, quadratic, solving quadratic equations

October 9, 2025 · 6:37 am

Trigonometric Exact Values

Find exactly $sin(18^\circ)$

We must be able to find an arithmetic combination of the exact values we knew to find $18$ .

$\begin{equation*}90=5\times 18\end{equation}$

$\begin{equation*}90-3(18)=2(18)\end{equation}$

I re-arranged as above, so I could take advantage of $cos(90)=0$ and $sin(90)=1$

cos(2x)=cos^2(x)-sin^2(x)=1-2sin^2(x)=2cos^2(x)-1

$\begin{equation*}sin(90-3(18))=sin(2(18))\end{equation}$

$\begin{equation*}sin(90)cos(3(18))-sin(3(18))cos(90)=2sin(18)cos(18)\end{equation}$

$\begin{equation*}cos(3(18))=2sin(18)cos(18)\end{equation}$

$\begin{equation*}4cos^3(18)-3cos(18)=2sin(18)cos(18)\end{equation}$

$\begin{equation*}4cos^3(18)-3cos(18)-2sin(18)cos(18)=0\end{equation}$

$\begin{equation*}cos(18)(4cos^2(18)-3-2sin(18))=0\end{equation}$

Hence,

$\begin{equation*}4cos^2(18)-2sin(18)-3=0\end{equation}$

$\begin{equation*}4-4sin^2(18)-2sin(18)-3=0\end{equation}$

$\begin{equation*}-4sin^2(18)-2sin(18)+1=0\end{equation}$

Use the quadratic equation formula

$\begin{equation*}sin(18)=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\end{equation}$

$\begin{equation*}sin(18)=\frac{2 \pm \sqrt{4-4(-4)(1)}}{-8}\end{equation}$

$\begin{equation*}sin(18)=\frac{2 \pm \sqrt{20}}{-8}\end{equation}$

$\begin{equation*}sin(18)=\frac{-2 \mp 2\sqrt{5}}{8}\end{equation}$

$\begin{equation*}sin(18)=\frac{-1 \mp \sqrt{5}}{4}\end{equation}$

As $sin(18)>0$ , $sin(18)=\frac{-1+\sqrt{5}}{4}$

Leave a Comment

Filed under Addition and Subtraction Identities, Algebra, Identities, Quadratic, Quadratics, Solving, Solving Equations, Solving Trig Equations, Trigonometry, Year 11 Specialist Mathematics

Tagged as exact values, sin(18), trig exact values, trigonometric identities

October 4, 2025 · 8:36 am

Converting base 10 numbers to base 2

Converting integers to base 2 is reasonably easy.

For example, what is 82 in base 2?

Think about powers of 2

$n$	$2^n$
$0$	$1$ (‘ones’)
$1$	$2$ (‘tens’)
$2$	$4$ (‘hundreds)
$3$	$8$ (‘thousands’)

Make $82$ the sum of powers of $2$ .

$82=64+16+2=1\times 2^6+0\times 2^5+ 1\times 2^4+0\times 2^3+0\times 2^2+1 \times 2^1+0\times 2^0=1010010$

We follow the same approach for real numbers

$n$	$2^n$
$-3$	$\frac{1}{8}=0.125$
$-2$	$\frac{1}{4}=0.25$
$-1$	$\frac{1}{2}=0.5$
$0$	$1$ (‘ones’)
$1$	$2$ (‘tens’)
$2$	$4$ (‘hundreds)
$3$	$8$ (‘thousands’)