Monthly Archives: September 2025

September 30, 2025 · 3:54 am

Geometry Problem

*Geometry Snacks* by Ed Southall and Vincent Pantaloni

I started by trisecting another side of the triangle

This makes it clearer that the two lines are parallel

Which means the two angles labelled above are corresponding and therefore congruent.

Let the side length be $x$ .

The area of the equilateral triangle is

(1) $\begin{equation*}A=\frac{1}{2}x^2 sin(60)=\frac{\sqrt{3}x^2}{4}\end{equation*}$

$\begin{equation*}cos(60)=\frac{y}{\frac{2x}{3}}\end{equation}$

$\begin{equation*}y=\frac{x}{3}\end{equation}$

Area of right triangle

(2) $\begin{equation*}A=(\frac{1}{2})(\frac{2x}{3})(\frac{x}{3})sin(60)=\frac{\sqrt{3}x^2}{18}\end{equation*}$

The fraction of the area is

$\begin{equation*}=\frac{\frac{\sqrt{3}x^2}{18}}{\frac{\sqrt{3}x^2}{4}}=\frac{2}{9}\end{equation}$

Leave a Comment

Filed under Algebra, Area, Area of Triangles (Sine), Finding an area, Geometry, Puzzles, Right Trigonometry, Simplifying fractions, Trigonometry

Tagged as geometry problem, geometry snacks

September 24, 2025 · 9:31 am

My Year 11 Specialist students have had an investigation which involves finding eigenvalues, eigenvectors and lines that are invariant under a particular linear transformation. This is not part of the course, but I feel for teachers who have to create new investigations every year.

Let’s find the eigenvalues and eigenvectors for matrix $T=\begin{bmatrix}-\frac{1}{2}&-\frac{\sqrt{3}}{2}\\-\frac{\sqrt{3}}{2}&\frac{1}{2}\end{bmatrix}$

We want to find $\lambda$ such that

(1) $\begin{equation*}T\textbf{v}=\lambda \textbf{v}\end{equation*}$

We solve $det(T-\lambda I)=0$

$\begin{equation*}T-\lambda I=\begin{bmatrix}-\frac{1}{2}-\lambda&-\frac{\sqrt{3}}{2}\\-\frac{\sqrt{3}}{2}&\frac{1}{2}-\lambda\end{bmatrix}\end{equation}$

$det\left (T-\lambda I \right )=\left (-\frac{1}{2}-\lambda \right ) \left ( \frac{1}{2}-\lambda \right )- \left (-\frac{\sqrt{3}}{2} \right ) \left ( -\frac{\sqrt{3}}{2} \right )$

Hence $0=\lambda^2-1$ and $\lambda=\pm 1$

When $\lambda=1$ , $\begin{bmatrix}-\frac{1}{2}&-\frac{\sqrt{3}}{2}\\-\frac{\sqrt{3}}{2}&\frac{1}{2}\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}x_1\\x_2\end{bmatrix}$

Hence, $-\frac{x_1}{2}-\frac{\sqrt{3}x_2}{2}=x_1$

$x_2=-\frac{3x_1}{\sqrt{3}}$ and the eigenvector is $\begin{bmatrix}1\\-\sqrt{3}\end{bmatrix}$

When $\lambda=-1$ , $\begin{bmatrix}-\frac{1}{2}&-\frac{\sqrt{3}}{2}\\-\frac{\sqrt{3}}{2}&\frac{1}{2}\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}-x_1\\-x_2\end{bmatrix}$

Hence, $-\frac{x_1}{2}-\frac{\sqrt{3}x_2}{2}=-x_1$

$x_2=\frac{x_1}{\sqrt{3}}$ and the eigenvector is $\begin{bmatrix}1\\\frac{1}{\sqrt{3}}\end{bmatrix}$

Which means the invariant lines are $y=-\sqrt{3}x$ and $y=\frac{x}{\sqrt{3}}$

A quadrilateral with vertices on our lines

The vertices after they have been transformed – A and C remain in the same place (they are on the $\lambda=1$ line)

The quadrilateral (purple) after the transformation

Leave a Comment

Filed under Co-ordinate Geometry, Eigenvalues, Matrices, Transformations, Vectors, Year 11 Specialist Mathematics

September 17, 2025 · 7:03 am

Divisibility Rule for 11

I was working on a question and involved 11 and I wondered what the divisibility rule was?

So then I had a bit of a think about it.

Let $N$ be a number divisible by $11$ . The $N (mod11)=0$

$\begin{equation*}N=a_n\times10^n+a_{n-1}\times10^{n-1}+a_{n-2}\times10^{n-2}+...+a_0\times10^0\end{equation}$

$\begin{equation*}0=a_n\times10^n (mod11)+a_{n-1}\times10^{n-1}(mod11)+a_{n-2}\times10^{n-2}(mod11)+...+a_0\times10^0(mod11)\end{equation}$

Now $10 (mod11)=10$ which is congruent to $-1$ because $10-(-1)=11$ , which is a multiple of 11.

Thus

$\begin{equation*}0=a_n(-1)^n+a_{n-1}(-1)^{n-1}+a_{n-2}(-1)^{n-2}+...+a_0(-1)^0\end{equation}$

Odd powers will be negative and even positive.

So if we start at one end of the number and add every second digit (i.e. first digit plus third digit plus fifth digit etc.) and then subtract the other digits (i.e. second digit, fourth digit, six digit, etc.), if that equals zero then the number is divisible by 11.

For example, is $1756238$ divisible by $11$ ?

$1+5+2+8-7-6-3=16-16=0$

Hence $1756238$ is divisible by $11$

Leave a Comment

Filed under Algebra, Arithmetic, Divisibility, Index Laws, Interesting Mathematics, Number Bases

Tagged as Divisibility rules, divisible by 11

September 15, 2025 · 3:12 am

Deriving the sum formula for an Arithmetic Progression

Arithmetic progressions (or arithmetic sequences) are sequences with a common difference (i.e. the same number is added or subtracted to get the next number in the sequence).

For example,

$2, 5, 8, 11, 14, ...$

$12,10, 8, 6, 4, ...$

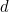The $n^{th}$ term of an arithmetic progression is $T_n=a+(n-1)d$ where $a$ is the first term and $d$ is the common difference.

i.e. For the sequence above, $T_4=12+(4-1)(-2)=6$

An arithmetic series is the sum of the arithmetic progression.

For example, if the sequence is

$3, 7, 11, 15, ...$

then $S_1=3, S_2=3+7=10, S_3=3+7+11=21$

The series is also a sequence and we are going to find the general term, $S_n$ .

$\begin{equation*}S_n=T_1+T_2+T_3+...+T_n\end{equation}$

which we can write as

$\begin{equation*}S_n=a+a+d+a+2d+...+a+(n-1)d\end{equation}$

Now, I am going to write that in reverse order (to make the next bit more obvious)

$\begin{equation*}S_n=a+(n-1)d+a+(n-2)d+a+(n-3)d+ ... +a\end{equation}$

I am going to add the two versions of $S_n$ together

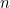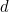Each term has an $a$ and there are $n$ terms, so we now have $2na$ . The $d$ terms, we going to group together

$d+(n-1)d+2d+(n-2)d+3d+(n-3)d+ ... +(n-1)d+d$

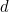Which simplifies to $nd+nd+nd+ ...+nd$ and we have $(n-1)$ $d$ terms. So this part of the sum is $(n-10nd$

Thus we have

$\begin{equation*}2S_n=2an+(n-1)nd\end{equation}$

Which simplifies to

(1) $\begin{equation*}S_n=\frac{n}{2}(2a+(n-1)d)\end{equation*}$

Let’s test it, remember the sequence $3, 7, 11, 15, ...$ . We know $S_3=21$

$\begin{equation*}S_3=\frac{3}{2}(2(3)+(3-1)(4))=\frac{3}{2}(14)=21\end{equation}$

Leave a Comment

Filed under Algebra, Arithmetic, Sequences, Year 11 Mathematical Methods

Tagged as arithmetic progressions, arithmetic sequences, arithmetic series, sequences

September 9, 2025 · 11:19 am

Linear Transformation (Rotation) Question

The unit square is rotated about the origin by $45^\circ$ anti-clockwise.
(a) Find the matrix of this transformation.
(b) Draw the unit square and its image on the same set of axes.
(c) Find the area of the over lapping region.

Remember the general rotation matrix is

$\begin{equation*}\begin{bmatrix}cos(\theta)&-sin(\theta)\\sin(\theta)&cos(\theta)\end{bmatrix}\end{equation}$

Hence

$\begin{equation*}\begin{bmatrix}cos(45)&-sin(45)\\sin(45)&cos(45)\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}\end{equation}$

The unit square has co-ordinates

$\begin{bmatrix}0 & 1 & 1& 0\\0&0&1&1\end{bmatrix}$

Transform the unit square

$\begin{bmatrix}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}\begin{bmatrix}0 & 1 & 1& 0\\0&0&1&1\end{bmatrix}=\begin{bmatrix}0&\frac{1}{\sqrt{2}}&0&-\frac{1}{\sqrt{2}}\\0&\frac{1}{\sqrt{2}}&\frac{2}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}$

The overlapping area is the area of $\Delta ADC$ – the area of $\Delta EFC$

We know $\angle{FCE}=45^\circ$ because the diagonal of a square bisects the angle.

We know $\angle{EFC}$ is a right angle as it’s on a straight line with the vertex of a square.

Hence $\Delta EFC$ is isosceles.

$\overline{AC}=\sqrt{1^2+1^2}=\sqrt{2}$ and $\overline{AF}=1$ , hence $\overline{FC}=\sqrt{2}-1$

$A_{\Delta ADC}=\frac{1}{2}(1)(1)=\frac{1}{2}$

$A_{\Delta ECF}=\frac{1}{2}(\sqrt{2}-1)(\sqrt{2}-1)$

Area of shaded region = $\frac{1}{2}-\frac{1}{2}(3-2\sqrt{2})=\sqrt{2}-1$

Leave a Comment

Filed under Area, Co-ordinate Geometry, Finding an area, Geometry, Matrices, Transformations, Year 11 Specialist Mathematics

Tagged as matrix tranformations, rotations

September 6, 2025 · 9:50 am

Clock (Geometry Question)

At what time after 2pm will the minute hand over take the hour hand?

Let the distance the minute hand moves be $x^\circ$ . Then the distance the hour hand moves is $x-60^\circ$ (The angle between the hands at 2pm is $60^\circ$ )

The rate the hour hand moves is $R_H=\frac{30}{60}=\frac{1}{2}^\circ$ per minute, and the rate the minute hand moves is $R_M=\frac{360}{60}=6^\circ$ per minute.

The time is the distance divided by the rate,

$\begin{equation*}\frac{x}{6}=\frac{x-60}{\frac{1}{2}}\end{equation}$

$\begin{equation*}\frac{x}{2}=6x-360\end{equation}$

$\begin{equation*}360=\frac{11x}{2}\end{equation}$

$\begin{equation*}x=65\frac{5}{11}^\circ\end{equation}$

As the minute hand moves $65\frac{5}{11}^\circ$ , the change in time is $65\frac{5}{11}^\circ \div 6=10$ minutes and $54$ seconds. Hence the time is $2:11$ pm

Leave a Comment

Filed under Finding an angle, Geometry, Puzzles

Tagged as geometry clock question

September 1, 2025 · 3:50 am

Area Problem

Two rectangular garden beds have a combined area of $40m^2$ . The larger bed has twice the perimeter of the smaller and the larger side of the smaller bed is equal to the smaller side of the larger bed. If the two beds are not similar, and if all edges are a whole number of metres, what is the length, in metres, of the longer side of the larger bed?
AMC 2007 S.14

Let’s draw a diagram

From the information in the question, we know

(1) $\begin{equation*}xy+xz=40\end{equation*}$

and

$\begin{equation*}2x+2y=4x+4z\end{equation}$

$\begin{equation*}x+y=2x+2z\end{equation}$

(2) $\begin{equation*}y=x+2z\end{equation*}$

Equation $1$ becomes

$\begin{equation*}x(x+3z)=40\end{equation}$

As the sides are whole numbers, consider the factors of 40.

$1, 2, 4, 5, 8, 10, 20, 40$

Remember $z<x<y$

$x$	$x+3z$	$z$	$y$	Perimeter Large	Perimeter Small	Comment
$2$	$20$	$6$				$x$ must be greater than $z$
$4$	$10$	$2$	$8$	$2(4+8)=24$	$2(2+4)=12$	This one works
$5$	$8$	$1$	$7$	$2(5+7)=24$	$2(5+1)=12$	This one also works
$8$	$10$	$\frac{2}{3}$				$z$ not a whole number
$10$	$4$	$z<0$				Not possible
$20$	$2$	$z<0$				Not possible
$40$	$1$	$z<0$				Not possible