Using an appropriate double angle identity, find the exact value of
The double angle identity for sine is
(1) ![]()
That means ![]() is either
is either ![]() or
or ![]() .
.
It must be ![]() as
as ![]() as there are exact values for
as there are exact values for ![]()
Hence,
![]()
![]()
![]()
![]()
![]()
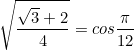
As ![]() is in the first quadrant, we don’t need to consider the negative version.
is in the first quadrant, we don’t need to consider the negative version.
![]()
