Combinations Proof

Prove $\begin{pmatrix}n+1\\r\end{pmatrix}=\begin{pmatrix}n\\r-1\end{pmatrix}+\begin{pmatrix}n\\r\end{pmatrix}$

Let’s start with the right hand side.

$RHS=\begin{pmatrix}n\\r-1\end{pmatrix}+\begin{pmatrix}n\\r\end{pmatrix}$

$RHS=\frac{n!}{(n-(r-1))!(r-1)!}+\frac{n!}{(n-r)!r!}$

Simplify

$RHS=\frac{n!}{(n+1-r)!}+\frac{n!}{(n-r)!r!}$

There is a common denominator of $(n+1-r)!r!$

$RHS=\frac{n!}{(n+1-r)!}\times \frac{r}{r}+\frac{n!}{(n-r)!r!}\times \frac{n+1-r}{n+1-r}$

$RHS=\frac{n!r+n!(n+1-r)}{(n+1-r)r!}$

$RHS=\frac{n!r+(n+1)n!-n!r}{(n+1-r)!r!}$

$RHS=\frac{(n+1)!}{(n+1-r)!r!}$

$RHS=\begin{pmatrix}n+1\\r\end{pmatrix}$

$RHS=LHS$

We know this intuitively from Pascal’s triangle

Where each entry is the sum of the two entries above it – for example,

$6+4=10$

Remember, Pascal’s triangle can be written as combinations,

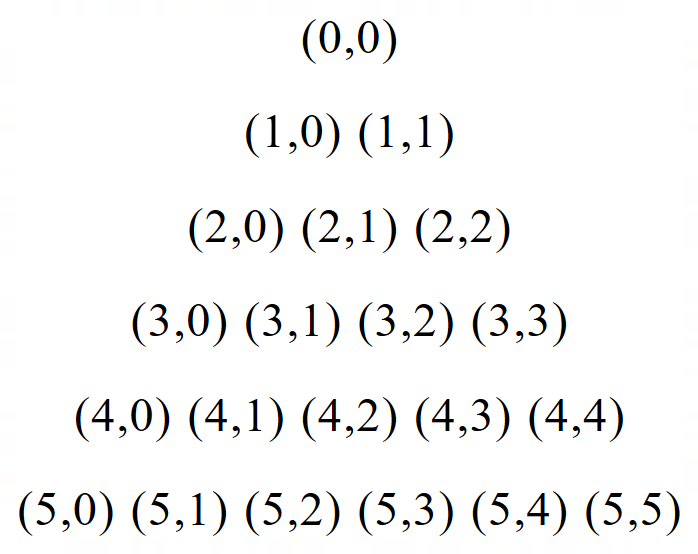
so $\begin{pmatrix}5\\3\end{pmatrix}=\begin{pmatrix}4\\2\end{pmatrix}+\begin{pmatrix}4\\3\end{pmatrix}$

Recent Posts