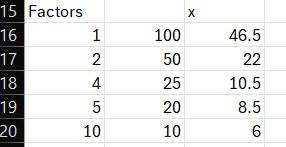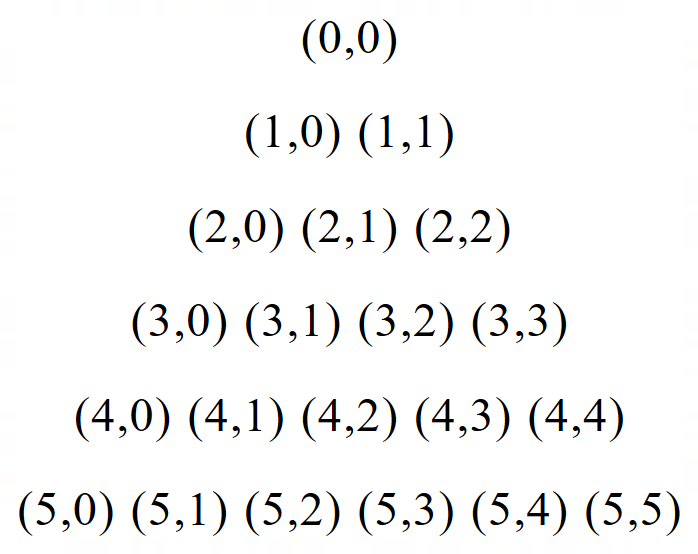How many three digit numbers can you form from the digits 1, 2, 3, 4 and 5 if
(a) the digits must occur in increasing order?
(b) adjacent digits differ by 2?
Cambridge Year 11 Specialist Mathematics Skill Sheet 1A
(a) There are ![]() permutations of three digits from the five digits, but how many of those are in the right order?
permutations of three digits from the five digits, but how many of those are in the right order?
Each set of 3 digits has 6 arrangements (![]() ).
).
For example, if the set is ![]() , then the possible arrangements are:
, then the possible arrangements are:
123, 132, 213, 231, 312, and 321.
Only one of those arrangements is in numerical order.
Hence what we want is ![]()
(b) I think this one is more about creating a list. I shall start with 1
135, 531, 131, 242, 353, 424, 535, 315
There are 8 possibilities.

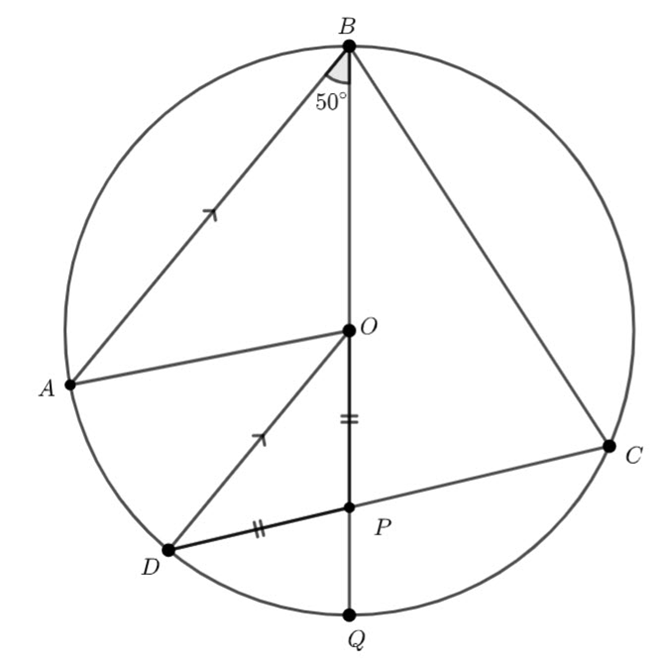
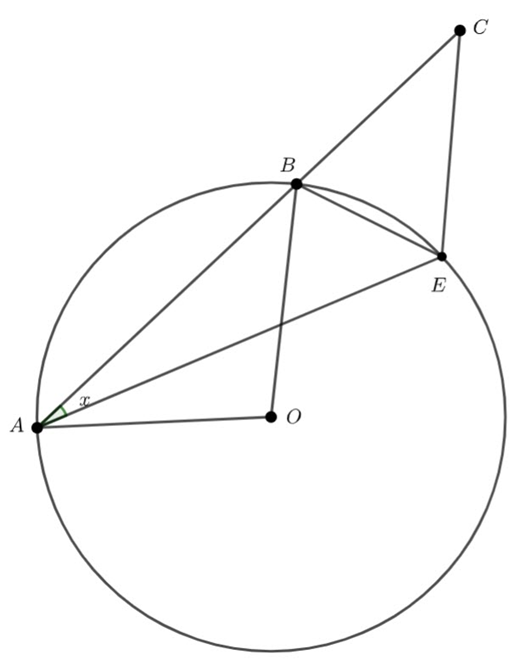

 values.
values.