Factorising Non-Monic Quadratics

The general equation of a quadratic is

Let’s explore different methods of factorising a non-monic quadratic (the term is not )

Factorise

We need to find two numbers that add to and multiply to (i.e. add to and multiply to

The two numbers are and

Method 1 – Splitting the middle term

This is the method I teach the most often

   

Split the middle term (the term) into the two numbers

   

The order doesn’t matter.

Find a common factor for the first term terms, and then for the last two terms.

   

There is a common factor of , factor it out.

   

Method two – Fraction

   

Put into both factors and divide by

   

Factorise

   

   

   

Method 3 – Monic to non-monic

   

Multiply both sides of the equation by

   

   

   

Let

   

Factorise

   

Replace the with

   

   

   

   

Method 4 – Cross Method

   

Place the two numbers in the cross

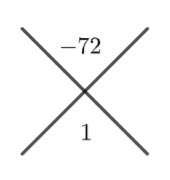
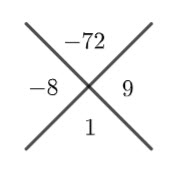
Place the two numbers that add to and multiply to in the other parts of the cross.

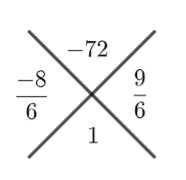
Divide these two numbers by (i.e )

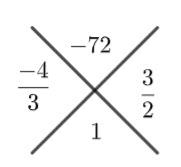
Simplify

Hence,

   

Which is

   

Method 5 – By Inspection

This is my least favourite method – although students get better with practice

   

The factors of are and and the factors of are

We know one number is positive and one number negative.

Which give us all of these possibilities

Possible factorisations	term of expansion
		No
		No
		No
		No
		No
		Almost, switch the signs
		Yes

   

With a bit of practice you don’t need to check all of the possibilties, but I find students struggle with this method.

Method 6 – Grid

   

Create a grid like the one below

Find the two numbers that multiply to and add to and place them in the other grid spots (see below)

Find the HCF (highest common factor) of each row and put in the first column.

Row HCF=, Row HCF=

For the columns, calculate what is required to multiple the HCF to get the table entry.

For example, what do you need to multiple and by to get and ? In this case it is . It’s always going to be the same thing, so just use one value to calculate it,

The factors are column and row

The two methods I use the most are splitting the middle term, and the cross method, but I can see value in the grid method.