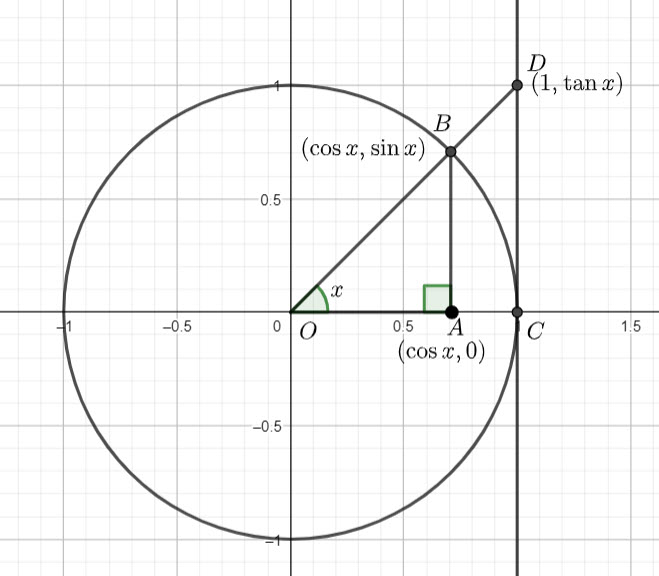
We are going to differentiate ![]() from first principals.
from first principals.
Remember the definition of a derivative is
(1) ![]()
If ![]() , then
, then
![]()
![]()
![]()
![]()
Let’s think about ![]()
Remember ![]() is defined as
is defined as ![]()
(2) ![]()
Let ![]() , as
, as ![]() hence
hence ![]()
If ![]() , then
, then ![]()
(3) ![]()
We are going to rewrite the equation ![]() as
as
(4) ![]()
And then we can write equation ![]() as
as
(5) ![]()
Using log laws we can write equation ![]() as
as
(6) ![]()
Let ![]()
As ![]()
equation ![]() becomes
becomes
(7) ![]()
We can move the limit to inside the natural log
(8) ![]()
And we know from the definition of ![]() that
that ![]()
Hence, equation ![]() is
is
(9) ![]()
Back to our derivative
![]()
We know that ![]() hence
hence
![]()