At 10am, object
travelling with constant velocity
km/h is sighted at the point with position vector
km. At 11am object
travelling with constant velocity
km/h is sighted at the point with position vector
km respectively. Use a scalar product method to determine
given that the two objects were closest together at a distance of
km at 4pm.
OT Lee Mathematics Specialist Year 11
At 4pm ![]() is at the point with position vector
is at the point with position vector ![]()
and ![]() is at the point with position vector
is at the point with position vector ![]()
We know the distance between ![]() and
and ![]() at 4pm is
at 4pm is ![]() km.
km.
Hence,
![]()
![]()
![]()
(1) ![]()
In the diagram below, I have found the position vector of ![]() relative to
relative to ![]()
![]() and the velocity of
and the velocity of ![]() relative to
relative to ![]()
![]()
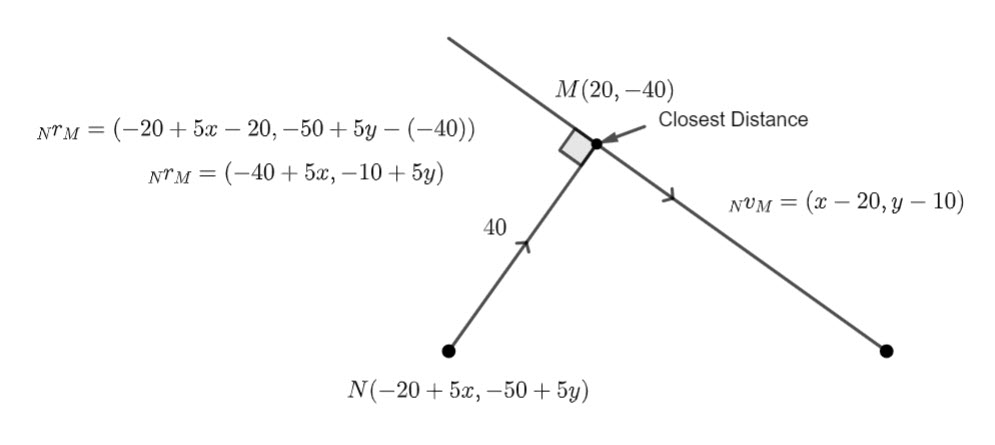
We know that when ![]()
![]() and
and ![]() are the closest distance apart.
are the closest distance apart.
![]()
![]()
![]()
(2) ![]()
Two equations and two unknowns which we can solve simultaneously. Both equations are circles.
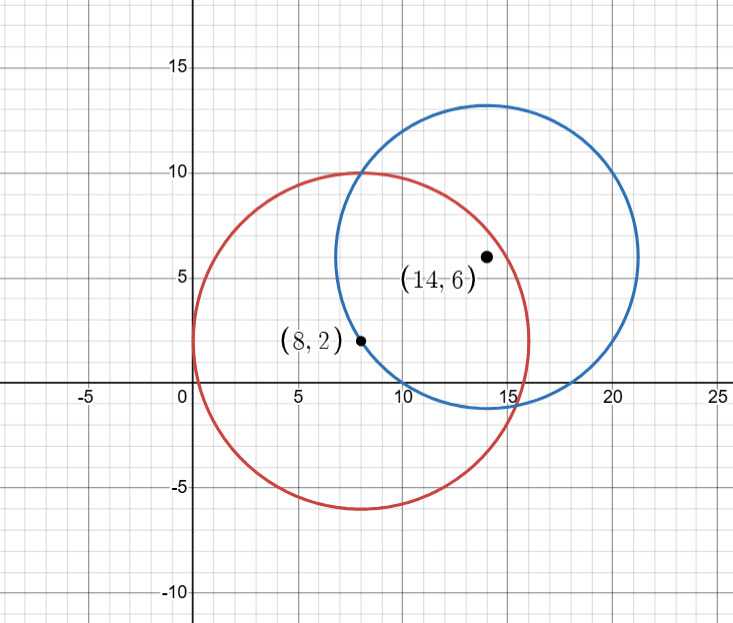
Equation ![]() becomes
becomes
(3) ![]()
and equation ![]() becomes
becomes
(4) ![]()
From equation ![]()
![]()
We will worry about the negative version later.
Substitute for ![]() into equation
into equation ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Square both sides of the equation
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(5) ![]()
Substitute ![]() into
into ![]()
![]()
(6) ![]()
Substitute ![]() into
into ![]()
![]()
(7) ![]()
Now we need to consider the negative version of ![]() . If you work through (like I did above) you end with the same equation for
. If you work through (like I did above) you end with the same equation for ![]() .
.
Hence our two values for ![]() are
are ![]() or
or ![]() .
.
Would someone be expected to do this in an exam? I hope not, but I think its worth doing.
