Category Archives: Solving

November 22, 2025 · 6:10 am

Polynomial Long Division

I usually choose to use synthetic division when factorising polynomials, but I know some teachers are unhappy when their students do this. So for completeness, here is my PDF for Polynomial Long Division.

Polynomial Long Division Download

Leave a Comment

Filed under Algebra, Cubics, Factorisation, Factorising, Factorising, Polynomials, Quadratics, Solving, Solving, Solving Equations, Year 11 Mathematical Methods

Tagged as polynomial long division, solving cubic equations

October 15, 2025 · 6:19 am

Hard Equation Solving Question

Find the value(s) of $k$ such that the equation below has two numerically equal but opposite sign solutions (e.g. $5$ and $-5$ ).

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{k-1}{k+1}\end{equation}$

$\begin{equation*}(x^2-2x)(k+1)=(k-1)(4x-1)\end{equation}$

$\begin{equation*}(k+1)x^2-2kx-2x=4kx-k-4x+1\end{equation}$

$\begin{equation*}(k+1)x^2-2kx-4kx-2x+4x-1=0\end{equation}$

$\begin{equation*}(k+1)^2x^2-(6k-2)x-1=0\end{equation}$

For there to be two numerically equal but opposite sign solutions, the $b$ term of the quadratic equation must be $0$ .

$\begin{equation*}6k-2=0\end{equation}$

Hence $k=\frac{1}{3}$ .

When $k=\frac{1}{3}$ the equation becomes

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{\frac{-2}{3}}{\frac{4}{3}}\end{equation}$

$\begin{equation*}\frac{x^2-2x}{4x-1}=\frac{-1}{2}\end{equation}$

$\begin{equation*}2x^2-4x=-4x+1\end{equation}$

$\begin{equation*}2x^2-1=0\end{equation}$

$\begin{equation*}x^2=\frac{1}{2}\end{equation}$

$\begin{equation*}x=\pm \frac{1}{\sqrt{2}}\end{equation}$

Leave a Comment

Filed under Algebra, Polynomials, Quadratic, Quadratics, Solving, Solving, Solving Equations

Tagged as hard algebra question, quadratic, solving quadratic equations

October 9, 2025 · 6:37 am

Trigonometric Exact Values

Find exactly $sin(18^\circ)$

We must be able to find an arithmetic combination of the exact values we knew to find $18$ .

$\begin{equation*}90=5\times 18\end{equation}$

$\begin{equation*}90-3(18)=2(18)\end{equation}$

I re-arranged as above, so I could take advantage of $cos(90)=0$ and $sin(90)=1$

sin(2x)=2sin(x)cos(x)

cos(2x)=cos^2(x)-sin^2(x)=1-2sin^2(x)=2cos^2(x)-1

$\begin{equation*}sin(90-3(18))=sin(2(18))\end{equation}$

$\begin{equation*}sin(90)cos(3(18))-sin(3(18))cos(90)=2sin(18)cos(18)\end{equation}$

$\begin{equation*}cos(3(18))=2sin(18)cos(18)\end{equation}$

$\begin{equation*}4cos^3(18)-3cos(18)=2sin(18)cos(18)\end{equation}$

$\begin{equation*}4cos^3(18)-3cos(18)-2sin(18)cos(18)=0\end{equation}$

$\begin{equation*}cos(18)(4cos^2(18)-3-2sin(18))=0\end{equation}$

Hence,

$\begin{equation*}4cos^2(18)-2sin(18)-3=0\end{equation}$

$\begin{equation*}4-4sin^2(18)-2sin(18)-3=0\end{equation}$

$\begin{equation*}-4sin^2(18)-2sin(18)+1=0\end{equation}$

Use the quadratic equation formula

$\begin{equation*}sin(18)=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\end{equation}$

$\begin{equation*}sin(18)=\frac{2 \pm \sqrt{4-4(-4)(1)}}{-8}\end{equation}$

$\begin{equation*}sin(18)=\frac{2 \pm \sqrt{20}}{-8}\end{equation}$

$\begin{equation*}sin(18)=\frac{-2 \mp 2\sqrt{5}}{8}\end{equation}$

$\begin{equation*}sin(18)=\frac{-1 \mp \sqrt{5}}{4}\end{equation}$

As $sin(18)>0$ , $sin(18)=\frac{-1+\sqrt{5}}{4}$

sin(18)=\frac{-1+\sqrt{5}}{4}

Leave a Comment

Filed under Addition and Subtraction Identities, Algebra, Identities, Quadratic, Quadratics, Solving, Solving Equations, Solving Trig Equations, Trigonometry, Year 11 Specialist Mathematics

Tagged as exact values, sin(18), trig exact values, trigonometric identities

March 31, 2025 · 7:14 am

Deriving the Quadratic Equation formula

My year 10 students have been learning how to complete the square with the idea of then deriving the quadratic equation formula.

The general equation for a quadratic is $y=ax^2+bx+c$

Completing the square,

$\begin{equation*}ax^2+bx+c\end{equation}$

Factorise out the leading coefficient (i.e. $a$ )

$\begin{equation*}a(x^2+\frac{bx}{a}+\frac{c}{a})\end{equation}$

Half the second term (i.e $\frac{b}{a}$ ) and subtract the square of the second term.

$\begin{equation*}a((x+\frac{b}{2a})^2-(\frac{b}{2a})^2+\frac{c}{a})\end{equation}$

$\begin{equation*}a((x+\frac{b}{2a})^2-\frac{b^2}{4a^2}+\frac{c}{a})\end{equation}$

Simplify

$\begin{equation*}a((x+\frac{b}{2a})^2-\frac{b^2}{4a^2}+\frac{4ac}{4a^2})\end{equation}$

$\begin{equation*}a((x+\frac{b}{2a})^2+\frac{-b^2+4ac}{4a^2})\end{equation}$

$\begin{equation*}a(x+\frac{b}{2a})^2+\frac{-b^2+4ac}{4a}\end{equation}$

Now let’s solve

$\begin{equation*}a(x+\frac{b}{2a})^2+\frac{-b^2+4ac}{4a}=0\end{equation}$

$\begin{equation*}a(x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a}\end{equation}$

$\begin{equation*}(x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a^2}\end{equation}$

$\begin{equation*}(x+\frac{b}{2a})=\pm \sqrt{\frac{b^2-4ac}{4a^2}}\end{equation}$

$\begin{equation*}(x+\frac{b}{2a})=\frac{\pm \sqrt{b^2-4ac}}{2a}\end{equation}$

$\begin{equation*}x=-\frac{b}{2a}\frac{\pm \sqrt{b^2-4ac}}{2a}\end{equation}$

Which is the quadratic equation formula.

Filed under Algebra, Quadratic, Quadratics, Solving, Solving, Solving Equations

Tagged as completing the square, quadratic equation formula

November 29, 2024 · 8:11 am

Interesting Equation

I think this one is doing the rounds, I first saw it here.

$\begin{equation*}2^x3^{x^2}=6\end{equation}$

$x=1$ is the obvious answer, $2^1\times 3^1=6$ , but are there more answers?

This was my approach

$\begin{equation*}ln(2^x3^{x^2})=ln(6)\end{equation}$

$\begin{equation*}ln(2^x)+ln(3^{x^2})=ln(6)\end{equation}$

$\begin{equation*}xln(2)+x^2ln(3)-ln(6)=0\end{equation}$

$\begin{equation*}ln(3)x^2+ln(2)x-ln(6)=0\end{equation}$

A quadratic equation.

Hence,

$\begin{equation*}x=\frac{-ln(2)\pm\sqrt{(ln(2))^2-4(ln(3))(ln(6))}}{2ln(3)}\end{equation}$

I then used my calculator

Hence $x=1$ 0r $x=-1.631$

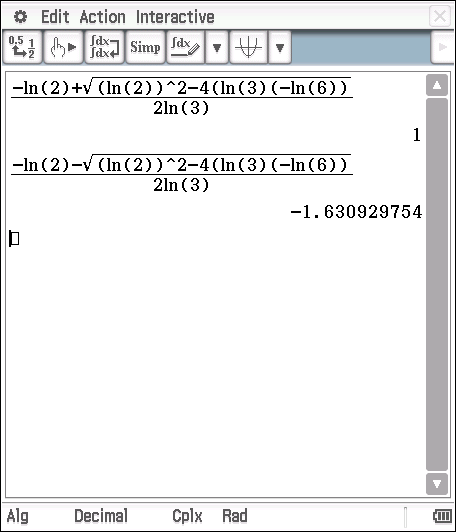
Leave a Comment

Filed under Algebra, Index Laws, Interesting Mathematics, Quadratics, Solving

Tagged as exponentials, index laws, Interesting maths, quadratic solving